Photo AI
Figure 3 shows a sketch of part of the curve with equation $y = 1 - 2 ext{cos} \, x$, where $x$ is measured in radians - Edexcel - A-Level Maths Pure - Question 18 - 2013 - Paper 1
Question 18
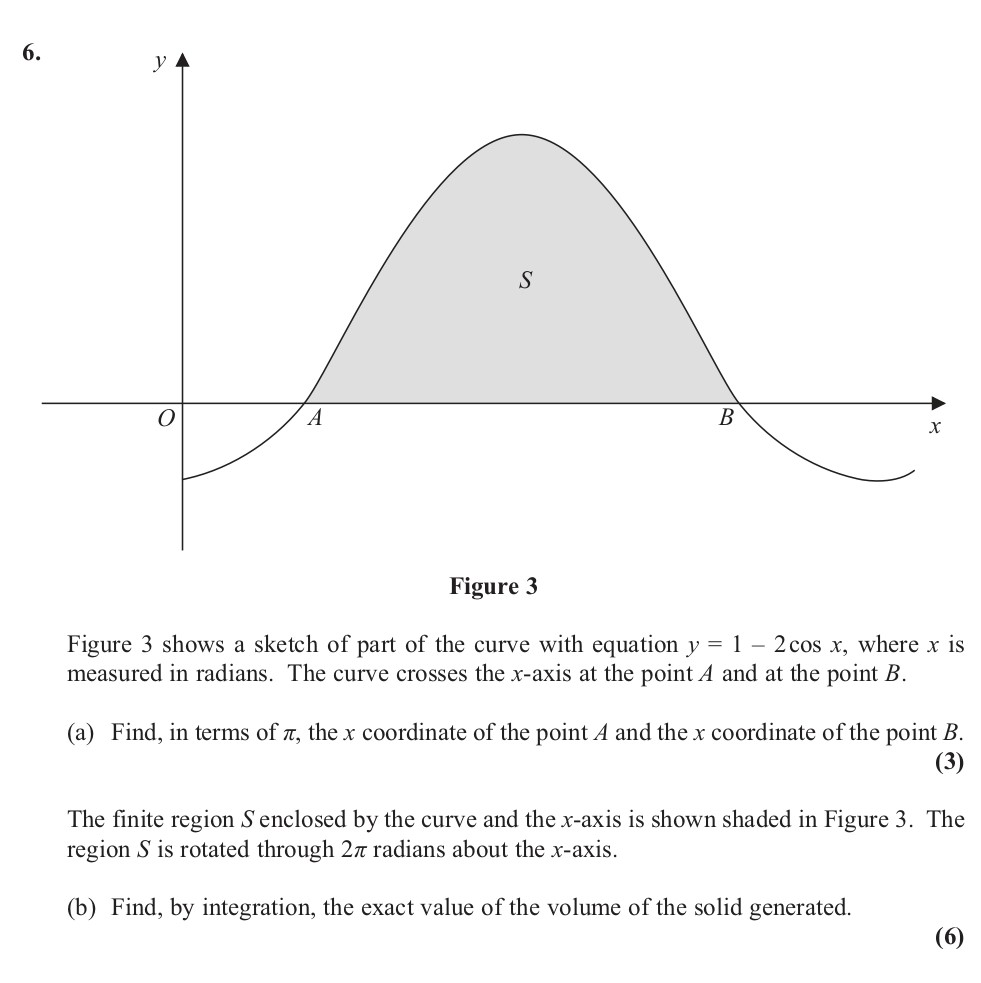
Figure 3 shows a sketch of part of the curve with equation $y = 1 - 2 ext{cos} \, x$, where $x$ is measured in radians. The curve crosses the $x$-axis at the point $... show full transcript
Worked Solution & Example Answer:Figure 3 shows a sketch of part of the curve with equation $y = 1 - 2 ext{cos} \, x$, where $x$ is measured in radians - Edexcel - A-Level Maths Pure - Question 18 - 2013 - Paper 1
Step 1
Step 2
Find, by integration, the exact value of the volume of the solid generated
Answer
To find the volume of the solid generated by rotating region about the -axis, we use the formula for volume:
Here, and the limits of integration are from to , which are rac{\pi}{3} and rac{5\pi}{3} respectively:
Now, calculating the integral:
-
Expand the square:
-
Therefore, we get:
-
Simplifying this results in:
-
Evaluating the integral produces the final volume value.
