Photo AI
Figure 1 shows part of the curve with equation $y = \, \sqrt{\tan x}$ - Edexcel - A-Level Maths Pure - Question 7 - 2007 - Paper 8
Question 7
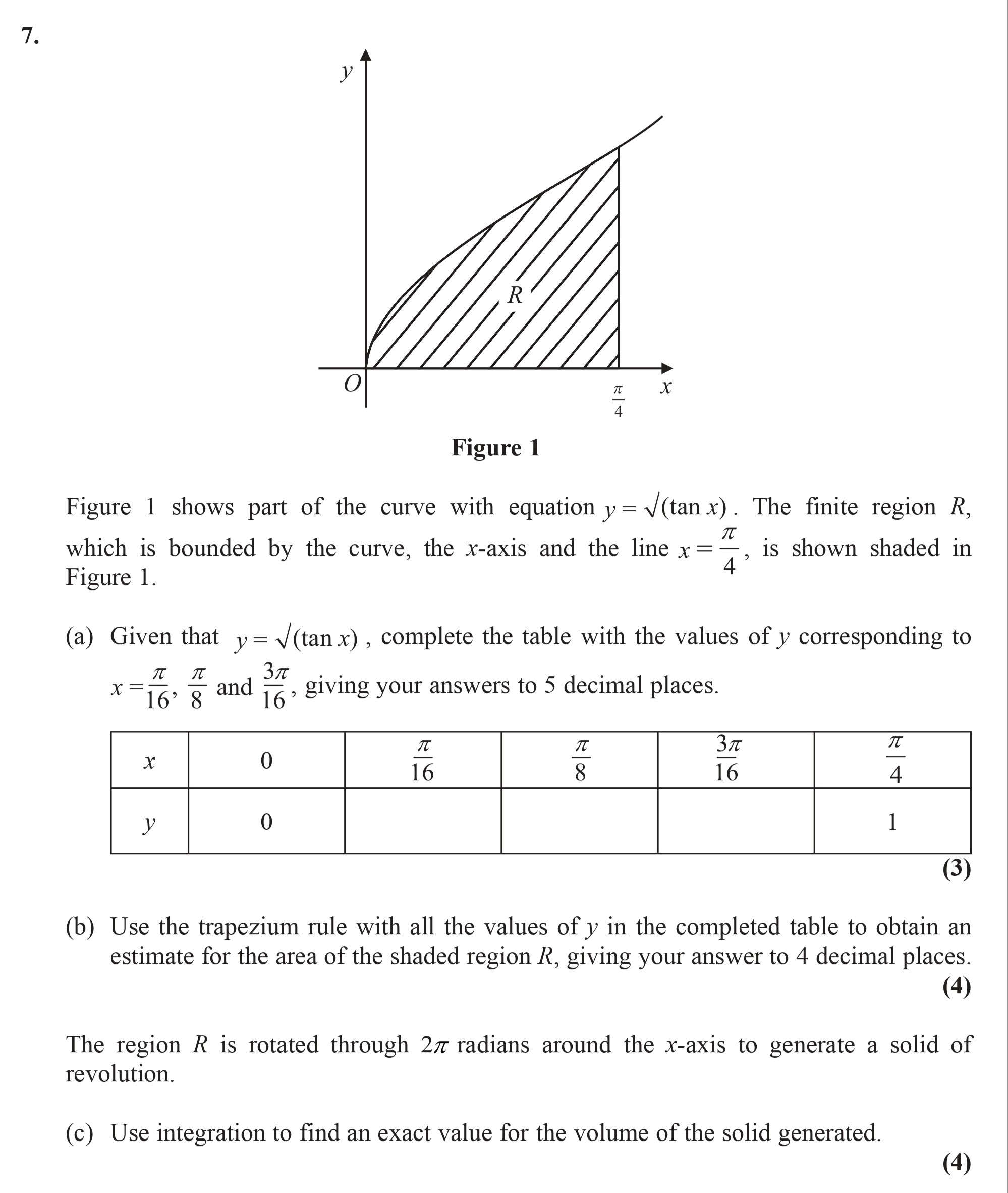
Figure 1 shows part of the curve with equation $y = \, \sqrt{\tan x}$. The finite region $\mathcal{R}$, which is bounded by the curve, the x-axis and the line $x = \... show full transcript
Worked Solution & Example Answer:Figure 1 shows part of the curve with equation $y = \, \sqrt{\tan x}$ - Edexcel - A-Level Maths Pure - Question 7 - 2007 - Paper 8
Step 1
Step 2
Use the trapezium rule with all the values of $y$ in the completed table to obtain an estimate for the area of the shaded region $\mathcal{R}$, giving your answer to 4 decimal places.
Answer
To use the trapezium rule, we calculate:
Area , where:
- for
- for
So,
Calculating this yields an area estimate of approximately .
Step 3
