8. (a) Find $ \int_0^{\frac{\pi}{4}} x \cos 4x \, dx $ (3) Figure 3 shows part of the curve with equation $ y = \sqrt{x} \sin 2x, \; x > 0 $ The finite region R, shown shaded in Figure 3, is bounded by the curve, the x-axis and the line with equation $ x = \frac{\pi}{4} $. The region R is rotated through $ 2\pi $ radians about the x-axis to form a solid of revolution. (b) Find the exact value of the volume of this solid of revolution, giving your answer in its simplest form. (Solutions based entirely on graphical or numerical methods are not acceptable.)

A-Level Edexcel Maths Pure Modelling with Functions: 8. (a) Find \( \int

8. (a) Find $ \int_0^{\frac{\pi}{4}} x \cos 4x \, dx $ (3) Figure 3 shows part of the curve with equation $ y = \sqrt{x} \sin 2x, \; x > 0 $ The finite region R, shown shaded in Figure 3, is bounded by the curve, the x-axis and the line with equation $ x = \frac{\pi}{4} $ - Edexcel - A-Level Maths Pure - Question 8 - 2018 - Paper 9

Question 8

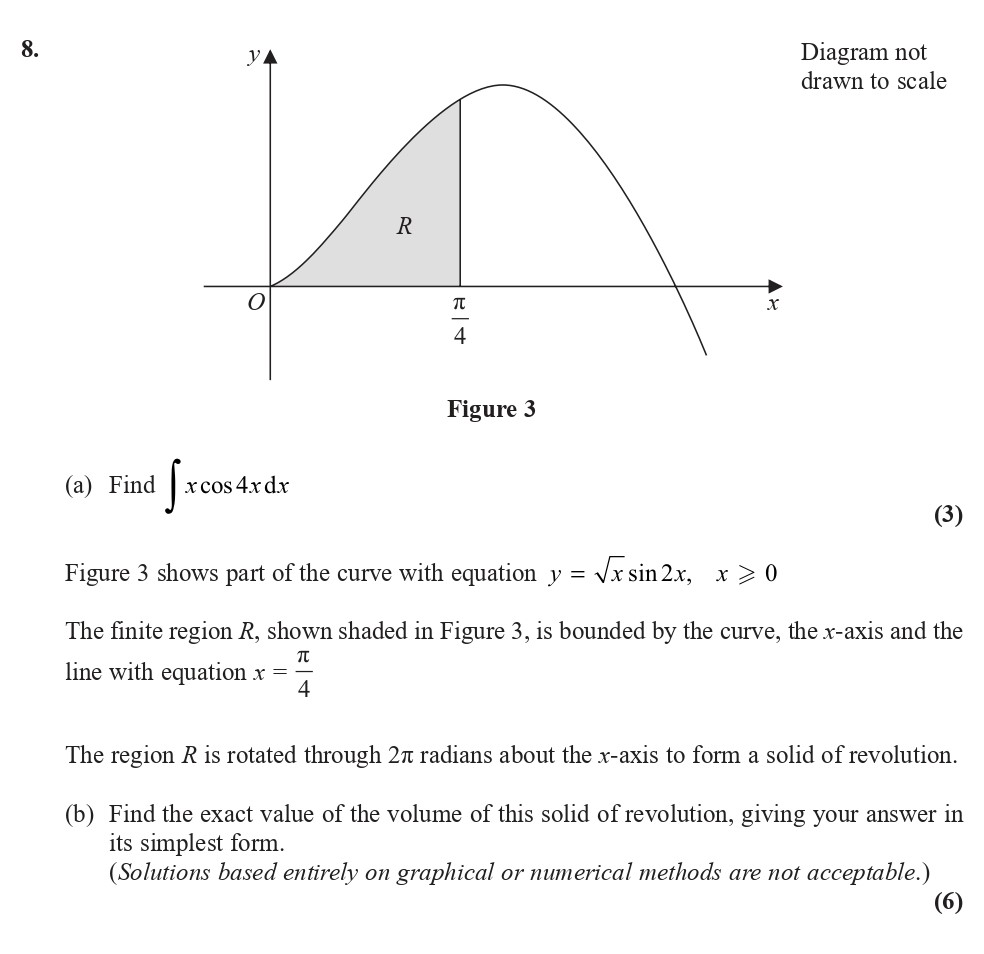
$8.-(a)-Find-$-\int_0^{\frac{\pi}{4}}-x-\cos-4x-\,-dx-$-(3)--Figure-3-shows-part-of-the-curve-with-equation-$-y-=-\sqrt{x}-\sin-2x,-\;-x->-0-$--The-finite-region-R,-shown-shaded-in-Figure-3,-is-bounded-by-the-curve,-the-x-axis-and-the-line-with-equation-$-x-=-\frac{\pi}{4}-$-Edexcel-A-Level Maths Pure-Question 8-2018-Paper 9.png$

8. (a) Find $ \int_0^{\frac{\pi}{4}} x \cos 4x \, dx $ (3) Figure 3 shows part of the curve with equation $ y = \sqrt{x} \sin 2x, \; x > 0 $ The finite region... show full transcript

Worked Solution & Example Answer:8. (a) Find $ \int_0^{\frac{\pi}{4}} x \cos 4x \, dx $ (3) Figure 3 shows part of the curve with equation $ y = \sqrt{x} \sin 2x, \; x > 0 $ The finite region R, shown shaded in Figure 3, is bounded by the curve, the x-axis and the line with equation $ x = \frac{\pi}{4} $ - Edexcel - A-Level Maths Pure - Question 8 - 2018 - Paper 9

Step 1

Find the volume of the solid of revolution

96%

114 rated

Answer

Next, we find the volume of the solid of revolution formed by rotating region R around the x-axis:

The volume ( V ) can be calculated using the disk method:

[ V = \pi \int_0^{\frac{\pi}{4}} \left( \sqrt{x} \sin 2x \right)^2 , dx ]

This results in:

[ V = \pi \int_0^{\frac{\pi}{4}} x \sin^2 2x , dx ]

Applying the integration by parts technique here as well, let:

( u = x )
( dv = \sin^2 2x , dx )

Use a trigonometric identity for ( \sin^2 ,): [ \sin^2 2x = \frac{1 - \cos 4x}{2} ]

Thus, [ V = \pi \int_0^{\frac{\pi}{4}} \left(\frac{x (1 - \cos 4x)}{2}\right) , dx ]

Using integration by parts on both terms and simplifying gives us: After evaluation, the exact volume is found to be:

[ V = \frac{\pi^2}{32} \text{ cubic units} ]

Find the volume of the solid of revolution

Join the A-Level students using SimpleStudy...