Photo AI
Figure 2 shows a sketch of the graph with equation y = 2|x + 4| - 5 The vertex of the graph is at the point P, shown in Figure 2 - Edexcel - A-Level Maths Pure - Question 11 - 2020 - Paper 2
Question 11
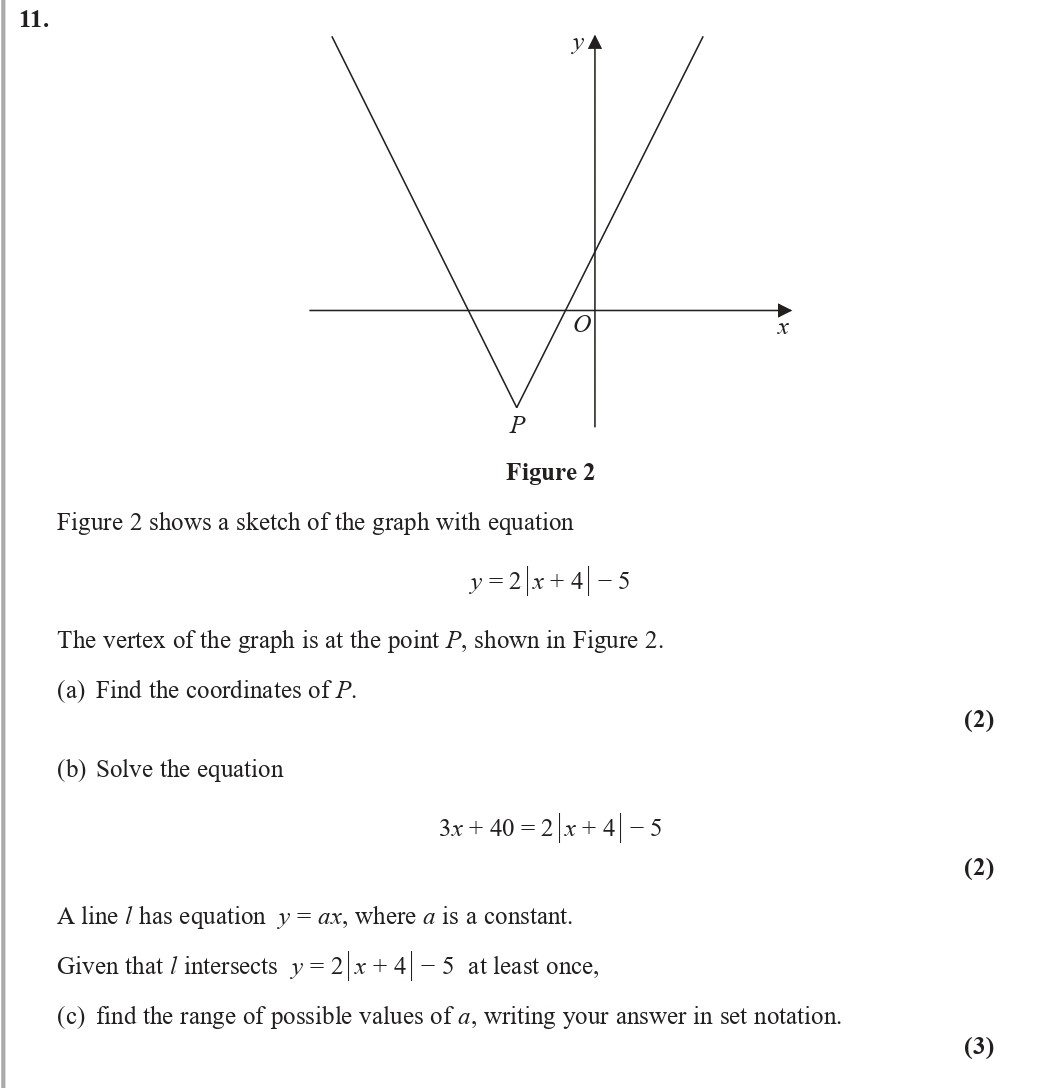
Figure 2 shows a sketch of the graph with equation y = 2|x + 4| - 5 The vertex of the graph is at the point P, shown in Figure 2. (a) Find the coordinates of P. ... show full transcript
Worked Solution & Example Answer:Figure 2 shows a sketch of the graph with equation y = 2|x + 4| - 5 The vertex of the graph is at the point P, shown in Figure 2 - Edexcel - A-Level Maths Pure - Question 11 - 2020 - Paper 2
Step 1
Step 2
Solve the equation 3x + 40 = 2|x + 4| - 5.
Answer
First, isolate the absolute value term:
Now we divide into two cases based on the definition of absolute values.
Case 1: For
Substituting this into the equation:
Case 2: For
Substituting this into the equation:
Thus, the solutions to the equation are and .
Step 3
Find the range of possible values of a, writing your answer in set notation.
Answer
To find the range of a, we consider the intersection of the lines:
Setting the equations equal to one another:
This will depend on the value of . The line will intersect the absolute function once if the slope does not exceed the steepness of the graph defined by:
We find the values of a for one intersection:
- From the vertex of the graph (), the maximum slope of the absolute function is 2.
- Solving gives us the intervals needed:
- For intersection:
- Also consider the line can cross between negative and positive segments.
Thus the final answer in set notation:
