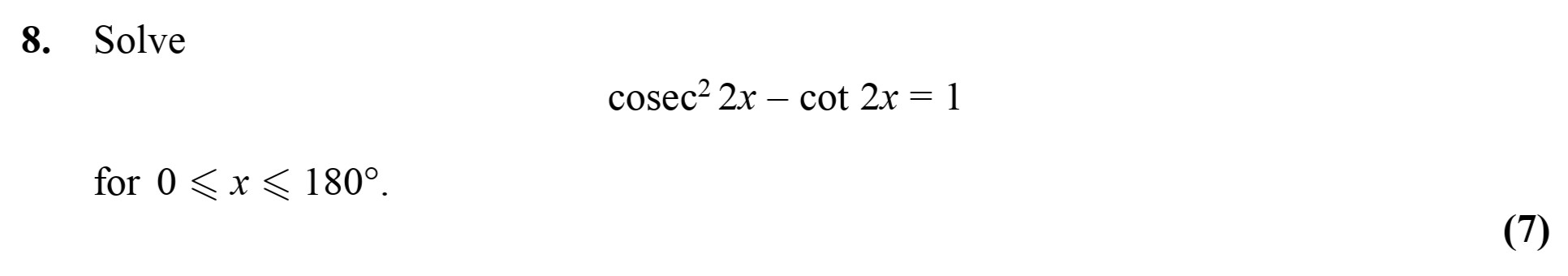Solve
cosec² 2x - cot 2x = 1
for 0 ≤ x ≤ 180°. - Edexcel - A-Level Maths Pure - Question 9 - 2010 - Paper 2

Question 9
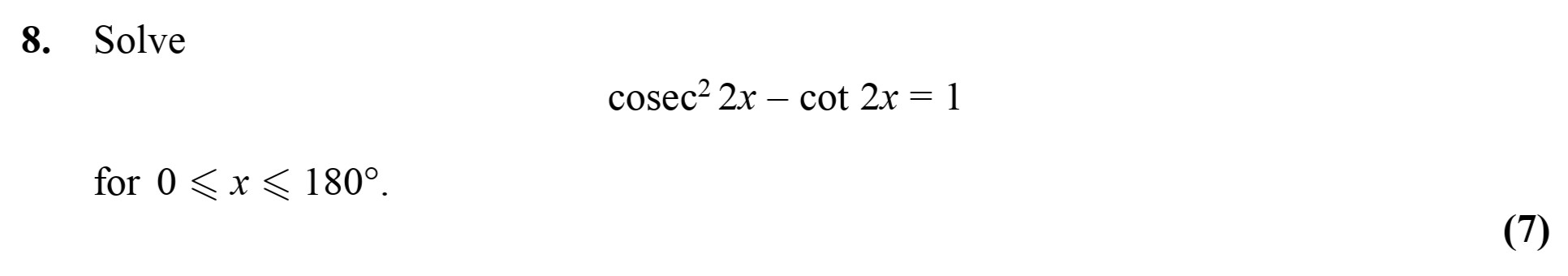
Solve
cosec² 2x - cot 2x = 1
for 0 ≤ x ≤ 180°.
Worked Solution & Example Answer:Solve
cosec² 2x - cot 2x = 1
for 0 ≤ x ≤ 180°. - Edexcel - A-Level Maths Pure - Question 9 - 2010 - Paper 2
Using cosec² 2x - cot 2x = 1

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
We start with the equation:
extcosec22x−extcot2x=1.
Using the identity for cosecant, we can rewrite the equation as:
1+extcot22x−extcot2x=1.
Simplifying this gives us:
extcot22x−extcot2x=0.Factoring the Equation

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
We can factor this expression:
extcot2x(extcot2x−1)=0.
Setting each factor to zero gives us two equations to solve:
extcot2x=0,
extcot2x−1=0.Solving cot 2x = 0

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
For the first equation,
extcot2x=0,
we find that this occurs when:
2x=90°+kimes180°,extwherekextisaninteger.
For the range 0 ≤ x ≤ 180°, we find:
2x=90°ightarrowx=45°,
2x=270°ightarrowx=135°.Solving cot 2x - 1 = 0

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
For the second equation:
extcot2x=1,
this occurs when:
2x=45°+kimes180°,extwherekextisaninteger.
In the range 0 ≤ x ≤ 180°, we derive:
2x=45°ightarrowx=22.5°,
2x=225°ightarrowx=112.5°.Final Solutions

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Combining all solutions obtained, we have:
x=22.5°,45°,112.5°,135°.
Thus, the final answers are:
extBothx=22.5°extandx=112.5°.Join the A-Level students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered