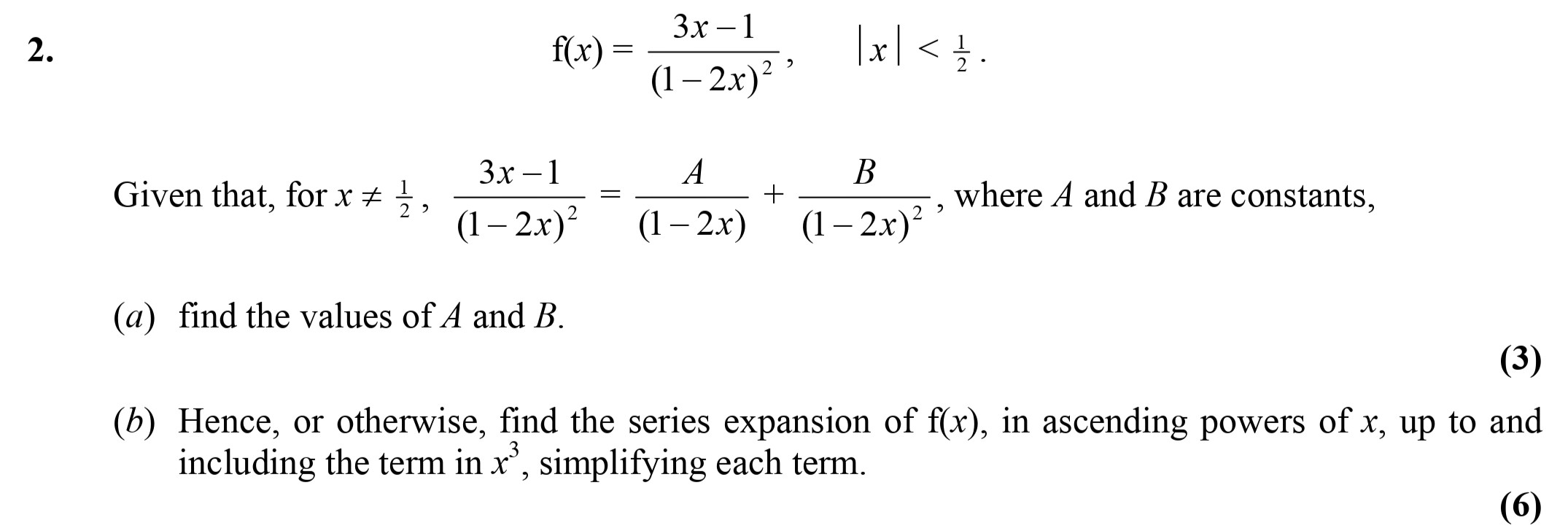f(x) = \frac{3x - 1}{(1 - 2x)^{2}} \quad |x| < \frac{1}{2}. Given that, for $x \neq \frac{1}{2},$ \n\frac{3x - 1}{(1 - 2x)^{2}} = \frac{A}{(1 - 2x)^{3}} + \frac{B}{(1 - 2x)^{2}}$ where A and B are constants, (a) find the values of A and B. (b) Hence, or otherwise, find the series expansion of f(x), in ascending powers of x, up to and including the term in $x^{3}$, simplifying each term.

A-Level Edexcel Maths Pure Parametric Equations: f(x) = \frac{3x - 1}{(1

f(x) = \frac{3x - 1}{(1 - 2x)^{2}} \quad |x| < \frac{1}{2} - Edexcel - A-Level Maths Pure - Question 4 - 2006 - Paper 6

Question 4

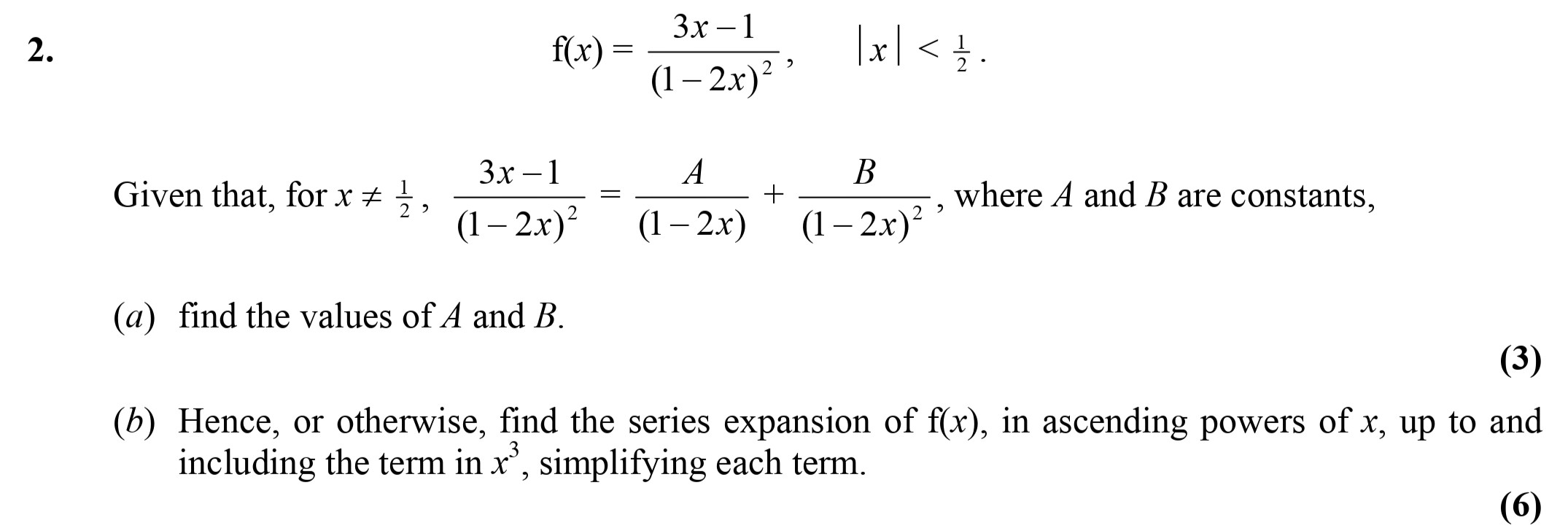
$f(x)-=-\frac{3x---1}{(1---2x)^{2}}--\quad-|x|-<-\frac{1}{2}-Edexcel-A-Level Maths Pure-Question 4-2006-Paper 6.png$

f(x) = \frac{3x - 1}{(1 - 2x)^{2}} \quad |x| < \frac{1}{2}. Given that, for $x \neq \frac{1}{2},$ \n\frac{3x - 1}{(1 - 2x)^{2}} = \frac{A}{(1 - 2x)^{3}} + \frac{B}... show full transcript

Worked Solution & Example Answer:f(x) = \frac{3x - 1}{(1 - 2x)^{2}} \quad |x| < \frac{1}{2} - Edexcel - A-Level Maths Pure - Question 4 - 2006 - Paper 6

Step 1

find the values of A and B.

96%

114 rated

Answer

To find the values of A and B, we first equate the two expressions.

Given the equation: $3x - 1 = A(1 - 2x) + B(1 - 2x)^{2}$ We can expand the right-hand side:

Expand: $A(1 - 2x) + B(1 - 2x)^{2} = A - 2Ax + B(1 - 4x + 4x^{2})$
$= A + B - (2A + 4B)x + 4Bx^{2}$
Combine like terms to equate coefficients:
- The constant term gives us: $A + B = -1$
- The coefficient of x gives us: $-(2A + 4B) = 3$
Solving these two equations:
- From the first equation, we can express B in terms of A: $B = -1 - A$
- Substitute B into the second equation: $-(2A + 4(-1 - A)) = 3$ $-2A + 4 + 4A = 3$ $2A = -1$ $A = -\frac{1}{2}$
- Substitute back to find B: $B = -1 - (-\frac{1}{2}) = -\frac{1}{2}$

Thus, the values are: $A = -\frac{1}{2}, B = -\frac{1}{2}$

Step 2

Hence, or otherwise, find the series expansion of f(x), in ascending powers of x, up to and including the term in $x^{3}$, simplifying each term.

99%

104 rated

Answer

To find the series expansion of f(x), we will first rewrite f(x) with the values of A and B we found:

$f(x) = \frac{3x - 1}{(1 - 2x)^{2}} = \frac{-\frac{1}{2}}{(1 - 2x)^{3}} + \frac{-\frac{1}{2}}{(1 - 2x)^{2}}$

Then, we will apply the binomial series expansion:

The binomial expansion for ( (1 - u)^{-n} ) is: $(1 - u)^{-n} = \sum_{k=0}^{\infty} \binom{n + k - 1}{k} u^{k}$ Valid for |u| < 1
For our case, using ( u = 2x ):
- For ( (1 - 2x)^{-2} ): $(1 - 2x)^{-2} = \sum_{k=0}^{\infty} \binom{1+k}{k} (2x)^{k} = 1 + 4x + 12x^{2} + 32x^{3} + \ldots$
- For ( (1 - 2x)^{-3} ): $(1 - 2x)^{-3} = \sum_{k=0}^{\infty} \binom{2+k}{k} (2x)^{k} = 1 + 6x + 24x^{2} + 64x^{3} + \ldots$
Combining the results:
- Therefore, substituting these into our function gives: $f(x) = -\frac{1}{2} \left[1 + 6x + 24x^{2} + 64x^{3} + \ldots\right] - \frac{1}{2} \left[1 + 4x + 12x^{2} + 32x^{3} + \ldots\right]$
- Simplifying: $= -\frac{1}{2}(2 + 10x + 36x^{2} + 96x^{3})$ $= -1 - 5x - 18x^{2} - 48x^{3}$

a final result: $f(x) = -1 - 5x - 18x^{2} - 48x^{3}$

f(x) = \frac{3x - 1}{(1 - 2x)^{2}} \quad |x| < \frac{1}{2} - Edexcel - A-Level Maths Pure - Question 4 - 2006 - Paper 6

Worked Solution & Example Answer:f(x) = \frac{3x - 1}{(1 - 2x)^{2}} \quad |x| < \frac{1}{2} - Edexcel - A-Level Maths Pure - Question 4 - 2006 - Paper 6

find the values of A and B.

Hence, or otherwise, find the series expansion of f(x), in ascending powers of x, up to and including the term in $x^{3}$, simplifying each term.

Join the A-Level students using SimpleStudy...