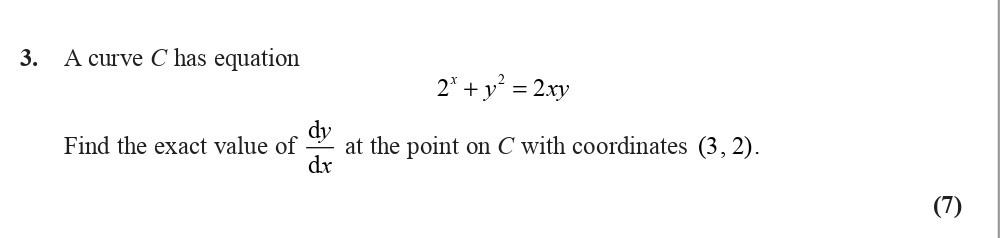Photo AI

A curve C has equation $2x^2 + y^2 = 2xy$ - Edexcel - A-Level Maths Pure - Question 5 - 2010 - Paper 6

Question icon

Question 5

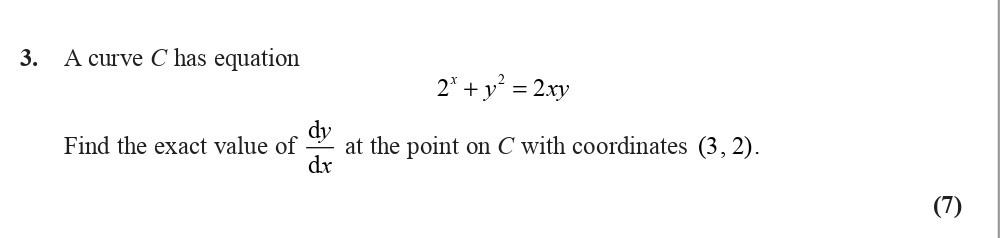
A-curve-C-has-equation--$2x^2-+-y^2-=-2xy$-Edexcel-A-Level Maths Pure-Question 5-2010-Paper 6.png

A curve C has equation $2x^2 + y^2 = 2xy$. Find the exact value of \( \frac{dy}{dx} \) at the point C with coordinates (3, 2).

Worked Solution & Example Answer:A curve C has equation $2x^2 + y^2 = 2xy$ - Edexcel - A-Level Maths Pure - Question 5 - 2010 - Paper 6

Step 1

Differentiate the equation

96%

114 rated

Answer

Differentiate both sides of the equation (2x^2 + y^2 = 2xy) with respect to (x):

ddx(2x2)+ddx(y2)=ddx(2xy)\frac{d}{dx}(2x^2) + \frac{d}{dx}(y^2) = \frac{d}{dx}(2xy)

Using the product rule on the right side, we have:

4x+2ydydx=2y+2xdydx4x + 2y \frac{dy}{dx} = 2y + 2x \frac{dy}{dx}

Step 2

Rearrange the equation

99%

104 rated

Answer

Rearranging gives us:

2ydydx−2xdydx=2y−4x2y \frac{dy}{dx} - 2x \frac{dy}{dx} = 2y - 4x

Factoring out (\frac{dy}{dx}):

(2y−2x)dydx=2y−4x(2y - 2x)\frac{dy}{dx} = 2y - 4x

Step 3

Solve for \( \frac{dy}{dx} \)

96%

101 rated

Answer

Now, solving for (\frac{dy}{dx}):

dydx=2y−4x2y−2x\frac{dy}{dx} = \frac{2y - 4x}{2y - 2x}

Step 4

Substituting (3, 2)

98%

120 rated

Answer

Substituting the coordinates ((3, 2)):

dydx=2(2)−4(3)2(2)−2(3)\frac{dy}{dx} = \frac{2(2) - 4(3)}{2(2) - 2(3)}

Calculating the numerator and denominator gives us:

dydx=4−124−6=−8−2=4\frac{dy}{dx} = \frac{4 - 12}{4 - 6} = \frac{-8}{-2} = 4

Join the A-Level students using SimpleStudy...

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;