Photo AI
A sequence of numbers $a_1, a_2, a_3, \ldots$ is defined by $$a_{n+1} = 5a_n - 3, \ n > 1$$ Given that $a_2 = 7$, (a) find the value of $a_1$ (b) Find the value of $$\sum_{r=1}^{4} a_r$$ - Edexcel - A-Level Maths Pure - Question 6 - 2014 - Paper 1
Question 6
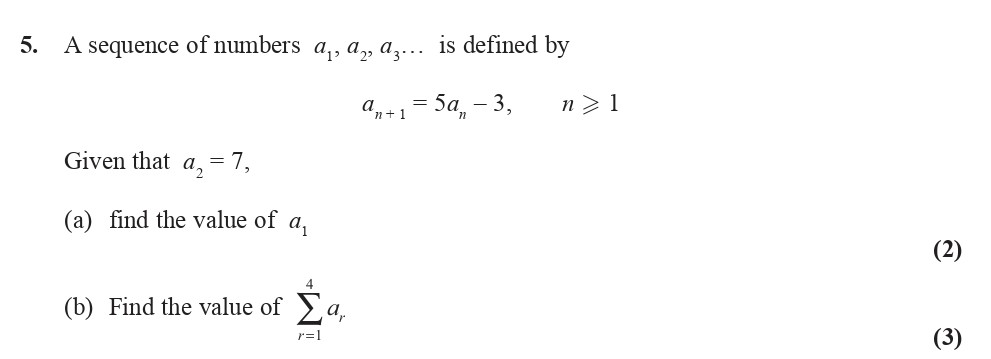
A sequence of numbers $a_1, a_2, a_3, \ldots$ is defined by $$a_{n+1} = 5a_n - 3, \ n > 1$$ Given that $a_2 = 7$, (a) find the value of $a_1$ (b) Find the ... show full transcript
Worked Solution & Example Answer:A sequence of numbers $a_1, a_2, a_3, \ldots$ is defined by $$a_{n+1} = 5a_n - 3, \ n > 1$$ Given that $a_2 = 7$, (a) find the value of $a_1$ (b) Find the value of $$\sum_{r=1}^{4} a_r$$ - Edexcel - A-Level Maths Pure - Question 6 - 2014 - Paper 1
Step 1
Step 2
Find the value of $\sum_{r=1}^{4} a_r$
Answer
We first need to determine the first four terms of the sequence:
- We have already found and .
- From earlier, we calculated . Now, let's find by substituting :
Now we have:
We can now compute the sum:
Calculating the sum step by step:
Thus, the value of the sum is 198.
