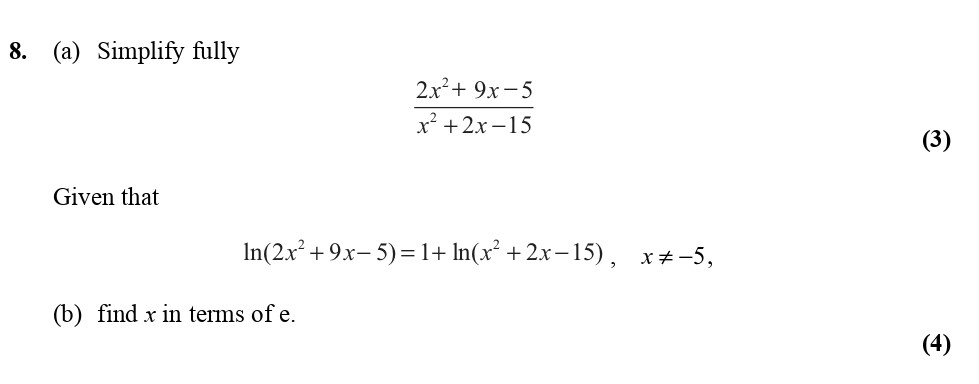8. (a) Simplify fully
$$\frac{2x^2 + 9x - 5}{x^2 + 2x - 15}$$
(3)
Given that
$$\ln(2x^2 + 9x - 5) = 1 + \ln(x^2 + 2x - 15), \quad x \neq -5,$$
(b) find x in terms of e - Edexcel - A-Level Maths Pure - Question 2 - 2010 - Paper 2

Question 2
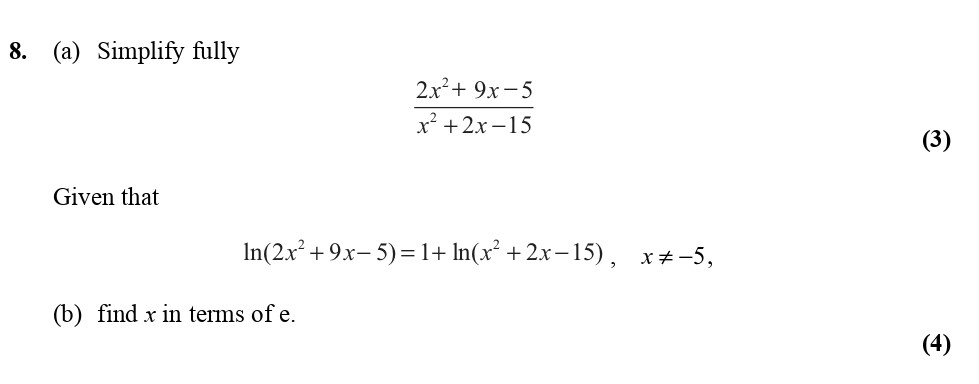
8. (a) Simplify fully
$$\frac{2x^2 + 9x - 5}{x^2 + 2x - 15}$$
(3)
Given that
$$\ln(2x^2 + 9x - 5) = 1 + \ln(x^2 + 2x - 15), \quad x \neq -5,$$
(b) find x in ter... show full transcript
Worked Solution & Example Answer:8. (a) Simplify fully
$$\frac{2x^2 + 9x - 5}{x^2 + 2x - 15}$$
(3)
Given that
$$\ln(2x^2 + 9x - 5) = 1 + \ln(x^2 + 2x - 15), \quad x \neq -5,$$
(b) find x in terms of e - Edexcel - A-Level Maths Pure - Question 2 - 2010 - Paper 2
(a) Simplify fully

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To simplify the expression x2+2x−152x2+9x−5, we will first factor both the numerator and denominator.
-
Factor the numerator:
- The expression 2x2+9x−5 factors into (2x−1)(x+5).
-
Factor the denominator:
- The expression x2+2x−15 factors into (x+5)(x−3).
-
Rewrite the original expression:
- Therefore, we can rewrite the fraction as:
(x+5)(x−3)(2x−1)(x+5).
-
Cancel the common factor:
- The (x+5) cancels out, resulting in:
x−32x−1.
Thus, the simplified expression is:
x−32x−1.
(b) find x in terms of e.

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To solve for x, we start with the given equation:
ln(2x2+9x−5)=1+ln(x2+2x−15).
-
Isolate the logarithmic expressions:
- Rewrite the equation as:
ln(2x2+9x−5)−ln(x2+2x−15)=1.
This simplifies further to:
ln(x2+2x−152x2+9x−5)=1.
-
Exponentiate both sides:
- Converting from logarithmic form gives:
x2+2x−152x2+9x−5=e1=e.
-
Cross-multiply:
- This leads to:
2x2+9x−5=e(x2+2x−15).
-
Expand and arrange the equation:
- Thus:
2x2+9x−5=ex2+2ex−15e.
Rearranging gives:
(2−e)x2+(9−2e)x+(15e−5)=0.
-
Use the quadratic formula:
- From the quadratic formula, we find:
x=2(2−e)−(9−2e)±(9−2e)2−4(2−e)(15e−5).
Thus, the value of x in terms of e is:
x=2(2−e)2e−9±(9−2e)2−4(2−e)(15e−5).
Join the A-Level students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered