Photo AI
The point P (4, -1) lies on the curve C with equation y = f(x), x > 0, and f'(x) = \frac{1}{2} - \frac{6}{\sqrt{x}} + 3 (a) Find the equation of the tangent to C at the point P, giving your answer in the form y = mx + c, where m and c are integers - Edexcel - A-Level Maths Pure - Question 8 - 2012 - Paper 2
Question 8
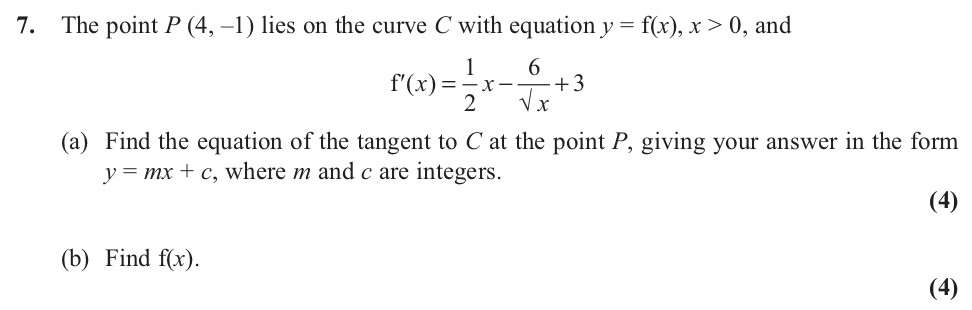
The point P (4, -1) lies on the curve C with equation y = f(x), x > 0, and f'(x) = \frac{1}{2} - \frac{6}{\sqrt{x}} + 3 (a) Find the equation of the tangent to C ... show full transcript
Worked Solution & Example Answer:The point P (4, -1) lies on the curve C with equation y = f(x), x > 0, and f'(x) = \frac{1}{2} - \frac{6}{\sqrt{x}} + 3 (a) Find the equation of the tangent to C at the point P, giving your answer in the form y = mx + c, where m and c are integers - Edexcel - A-Level Maths Pure - Question 8 - 2012 - Paper 2
Step 1
Find the equation of the tangent to C at the point P
Answer
To find the equation of the tangent, we first need to calculate the derivative at the point P. We have:
- Calculate f'(4):
f'(4) = \frac{1}{2} - \frac{6}{\sqrt{4}} + 3
= \frac{1}{2} - \frac{6}{2} + 3
= \frac{1}{2} - 3 + 3
= \frac{1}{2}
-
The slope m of the tangent at point P is therefore ( m = \frac{1}{2} ).
-
Now we use the point-slope form of a line equation:
y - y_1 = m(x - x_1)
where ( P(4, -1) ) gives us ( y_1 = -1 ) and ( x_1 = 4 ). -
Substituting the values: y - (-1) = \frac{1}{2}(x - 4)
y + 1 = \frac{1}{2}x - 2
y = \frac{1}{2}x - 3 -
To express in the form y = mx + c with integers, we write:
y = \frac{1}{2}x - 3 or equivalently:
2y = x - 6
which simplifies to y = \frac{1}{2}x - 3, where m = 1 and c = -3.
Step 2
Find f(x)
Answer
Given:
f'(x) = \frac{1}{2} - \frac{6}{\sqrt{x}} + 3
We need to integrate f'(x) to find f(x):
f(x) = \int f'(x) , dx
= \int \left( \frac{1}{2} - \frac{6}{\sqrt{x}} + 3 \right) , dx
= \frac{1}{2} x - 6 \int x^{-\frac{1}{2}} , dx + 3x + c
= \frac{1}{2} x - 12 \sqrt{x} + 3x + c
= \frac{1}{2} x + 3x - 12 \sqrt{x} + c
Now, substituting point P(4, -1) to find c:
f(4) = \frac{1}{2}(4) + 3(4) - 12 \sqrt{4} + c
-1 = 2 + 12 - 24 + c
c = -1 - 2 - 12 + 24
c = 7.
Thus, the function is: f(x) = \frac{1}{2}x + 3x - 12\sqrt{x} + 7.
