Photo AI
Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$ - Edexcel - A-Level Maths Pure - Question 10 - 2019 - Paper 1
Question 10
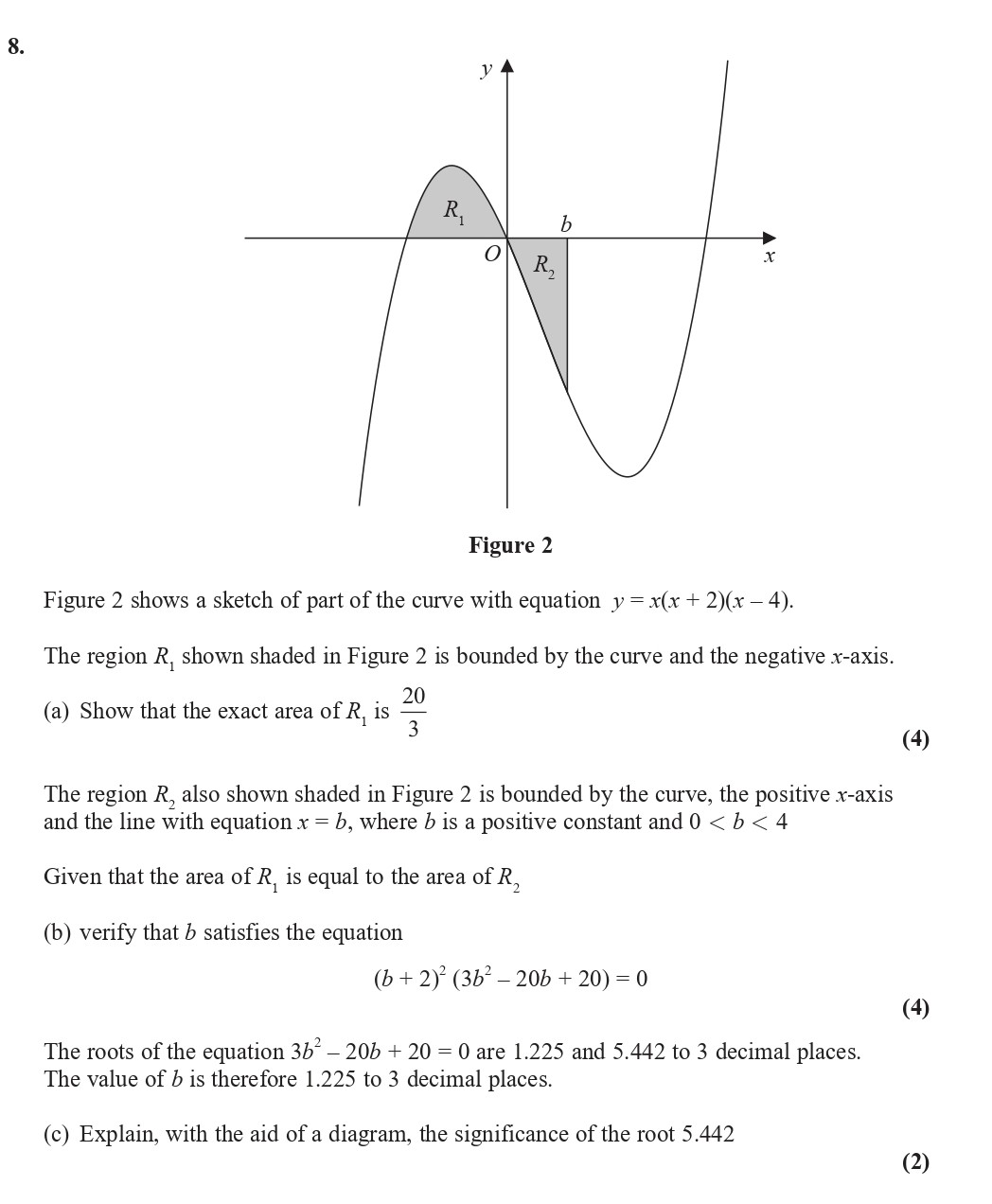
Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$. The region $R_1$, shown shaded in Figure 2 is bounded by the curve and the... show full transcript
Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$ - Edexcel - A-Level Maths Pure - Question 10 - 2019 - Paper 1
Step 1
Show that the exact area of $R_1$ is \( \frac{20}{3} \)
Answer
To find the area of the region , first we need to determine the points where the curve intersects the x-axis. This occurs when
,
which gives roots at , , and .
Next, we can calculate the area between and by integrating the curve:
We expand the integrand:
Thus, the area becomes:
Evaluating this integral gives:
Calculating at the bounds leads to:
Calculating each term results in:
Thus, the area .
Step 2
verify that $b$ satisfies the equation \( (b + 2)^2 (3b^2 - 20b + 20) = 0 \)
Answer
Starting from the equation for the area of , we know that it is equal to .
The integral for can be expressed as:
Evaluating this integral results in an expression set equal to , from which we can derive:
After simplifying the integral and substituting , we arrive at the equation
Breaking this down leads to the necessity for either factor to equal zero for a valid .
Step 3
Explain, with the aid of a diagram, the significance of the root 5.442.
Answer
The root 5.442 indicates the x-coordinate where the area defined above the x-axis for equals the area defined below the x-axis for .
Graphically, on the curve, this point of intersection highlights where the area under the curve for from to the point of intersection yields an area equal to as well.
Hence, this point represents a balance of areas between the shaded regions and and can be verified through appropriate diagram illustrations.
