Figure 2 shows a sketch of part of the graph $y = f(x)$, where $f(x) = 2/3 - |x| + 5, \, x \geq 0$ (a) State the range of $f$. (b) Solve the equation $f(x) = \frac{1}{2}x + 30$ (c) Given that the equation $f(x) = k$, where $k$ is a constant, has two distinct roots, (e) state the set of possible values for $k$.

A-Level Edexcel Maths Pure Proof: Figure 2 shows a sketch of part

Figure 2 shows a sketch of part of the graph $y = f(x)$, where $f(x) = 2/3 - |x| + 5, \, x \geq 0$ (a) State the range of $f$ - Edexcel - A-Level Maths Pure - Question 9 - 2017 - Paper 2

Question 9

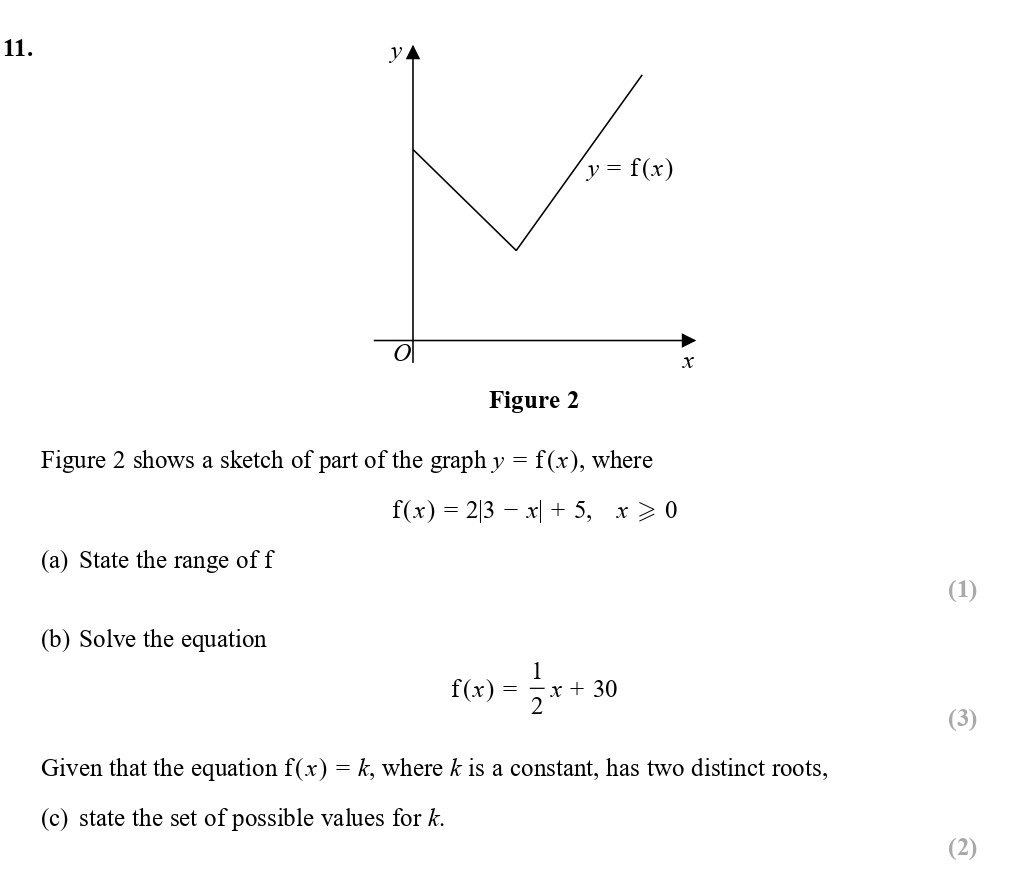
$Figure-2-shows-a-sketch-of-part-of-the-graph-$y-=-f(x)$,-where--$f(x)-=-2/3---|x|-+-5,-\,-x-\geq-0$--(a)-State-the-range-of-$f$-Edexcel-A-Level Maths Pure-Question 9-2017-Paper 2.png$

Figure 2 shows a sketch of part of the graph $y = f(x)$, where $f(x) = 2/3 - |x| + 5, \, x \geq 0$ (a) State the range of $f$. (b) Solve the equation $f(x) = \fr... show full transcript

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the graph $y = f(x)$, where $f(x) = 2/3 - |x| + 5, \, x \geq 0$ (a) State the range of $f$ - Edexcel - A-Level Maths Pure - Question 9 - 2017 - Paper 2

Step 1

State the range of $f$

96%

114 rated

Answer

The function $f(x)$ is composed of a linear function with a maximum at $5$ . Therefore, as the absolute value of $x$ increases, $f(x)$ decreases. The minimum value of $f(x)$ occurs when $x o rac{2}{3}$ , where the function approaches the value $5$ . Thus, the range of $f$ is:

$f(x) \geq 5.$

In interval notation, this can be expressed as $[5, \infty)$ .

Step 2

Solve the equation $f(x) = \frac{1}{2}x + 30$

99%

104 rated

Answer

To solve the equation, we start with:

$-2(3 - x) + 5 = \frac{1}{2}x + 30$

Expanding the left side:

$-6 + 2x + 5 = \frac{1}{2}x + 30$

Simplifying gives:

$2x - \frac{1}{2}x = 30 + 6 - 5$

Multiplying both sides by $2$ to eliminate the fraction:

$4x - x = 62$

Thus, we get:

$x = \frac{62}{3}.$

This corresponds to the solution of the equation.

Step 3

State the set of possible values for $k$

96%

101 rated

Answer

For the function $f(x)$ to have two distinct roots, it must intersect the horizontal line $y = k$ at two points. Observing the graph, the maximum point occurs at $y = 5$ and the function approaches $y = 11$ when $x o 0$ . Thus, for $f(x)$ to intersect twice, $k$ must satisfy:

$5 < k < 11$

In interval notation, the set of possible values for $k$ is:

$\{ k : 5 < k < 11 \}.$

Figure 2 shows a sketch of part of the graph $y = f(x)$, where $f(x) = 2/3 - |x| + 5, \, x \geq 0$ (a) State the range of $f$ - Edexcel - A-Level Maths Pure - Question 9 - 2017 - Paper 2

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the graph $y = f(x)$, where $f(x) = 2/3 - |x| + 5, \, x \geq 0$ (a) State the range of $f$ - Edexcel - A-Level Maths Pure - Question 9 - 2017 - Paper 2

State the range of $f$

Solve the equation $f(x) = \frac{1}{2}x + 30$

State the set of possible values for $k$

Join the A-Level students using SimpleStudy...