f(x) = \frac{3x - 1}{(1 - 2x)^2} \\[ |x| < \frac{1}{2} \\ Given that, for x ≠ \frac{1}{2}, \frac{3x - 1}{(1 - 2x)^2} = \frac{A}{(1 - 2x)} + \frac{B}{(1 - 2x)^2}, where A and B are constants, (a) find the values of A and B. \\ (b) Hence, or otherwise, find the series expansion of f(x), in ascending powers of x, up to and including the term in x³, simplifying each term.

A-Level Edexcel Maths Pure Radian Measure: f(x) = \frac{3x - 1}{(1

f(x) = \frac{3x - 1}{(1 - 2x)^2} \\[ |x| < \frac{1}{2} \\ Given that, for x ≠ \frac{1}{2}, \frac{3x - 1}{(1 - 2x)^2} = \frac{A}{(1 - 2x)} + \frac{B}{(1 - 2x)^2}, where A and B are constants, (a) find the values of A and B - Edexcel - A-Level Maths Pure - Question 3 - 2006 - Paper 6

Question 3

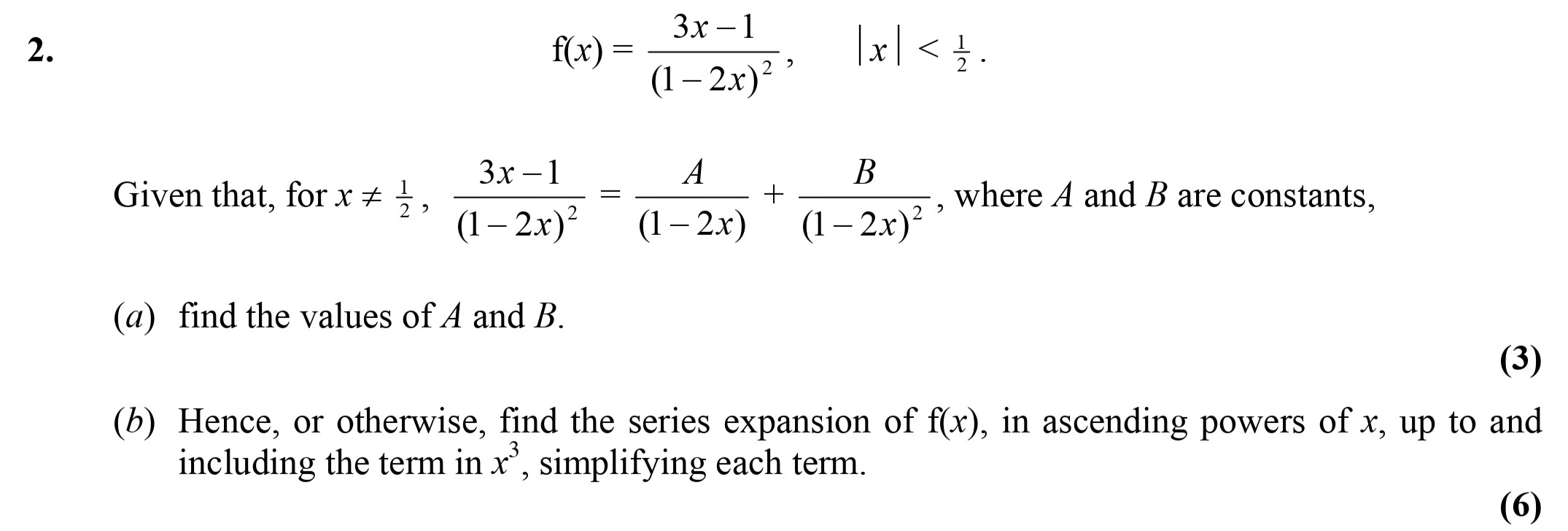
$f(x)-=-\frac{3x---1}{(1---2x)^2}-\\[-|x|-<-\frac{1}{2}-\\--Given-that,-for-x-≠-\frac{1}{2},-\frac{3x---1}{(1---2x)^2}-=-\frac{A}{(1---2x)}-+-\frac{B}{(1---2x)^2},-where-A-and-B-are-constants,----(a)-find-the-values-of-A-and-B-Edexcel-A-Level Maths Pure-Question 3-2006-Paper 6.png$

f(x) = \frac{3x - 1}{(1 - 2x)^2} \\[ |x| < \frac{1}{2} \\ Given that, for x ≠ \frac{1}{2}, \frac{3x - 1}{(1 - 2x)^2} = \frac{A}{(1 - 2x)} + \frac{B}{(1 - 2x)^2}, wh... show full transcript

Worked Solution & Example Answer:f(x) = \frac{3x - 1}{(1 - 2x)^2} \\[ |x| < \frac{1}{2} \\ Given that, for x ≠ \frac{1}{2}, \frac{3x - 1}{(1 - 2x)^2} = \frac{A}{(1 - 2x)} + \frac{B}{(1 - 2x)^2}, where A and B are constants, (a) find the values of A and B - Edexcel - A-Level Maths Pure - Question 3 - 2006 - Paper 6

Step 1

find the values of A and B.

96%

114 rated

Answer

To find the constants A and B, we start by equating the two sides of the given equation:

$3x - 1 = A(1 - 2x) + B$

Expanding the right-hand side gives us:

$3x - 1 = A - 2Ax + B$

Rearranging terms, we can group like terms:

$(3 + 2A)x + (A + B) = 0$

To satisfy the identity for all x, we need the coefficients of like terms to be equal, giving us:

For the coefficient of x: $A = -\frac{3}{2}$$$
For the constant term: $-1 = A + B$ Substituting A, we get: $B = -1 + \frac{3}{2} = \frac{1}{2}$$$

Thus, the values are:

$A = -\frac{3}{2}, B = \frac{1}{2}$

Step 2

Hence, or otherwise, find the series expansion of f(x), in ascending powers of x, up to and including the term in x³, simplifying each term.

99%

104 rated

Answer

To find the series expansion of f(x), we can substitute the values of A and B back into the expression derived:

Replacing, we have:

$f(x) = \frac{3x - 1}{(1 - 2x)^2} = \frac{-\frac{3}{2}}{(1 - 2x)} + \frac{\frac{1}{2}}{(1 - 2x)^2}$

Next, we apply the binomial series expansion for each term:

For (\frac{1}{1 - 2x}): $\frac{1}{1 - 2x} = 1 + 2x + 4x^2 + 8x^3 + \cdots$
For (\frac{1}{(1 - 2x)^2}): The expansion is given by the formula: ( (1 - 2x)^{-2} = \sum_{n=0}^{\infty} \binom{n + 1}{1}(2x)^n = 1 + 4x + 12x^2 + 32x^3 + \cdots )

Combining these expansions, we get:

$f(x) = -\frac{3}{2} (1 + 2x + 4x^2 + 8x^3) + \frac{1}{2} (1 + 4x + 12x^2 + 32x^3)$

Simplifying each term:

For the constant term: - $-\frac{3}{2} + \frac{1}{2} = -1$
For x term: - $-3 + 2 = -1$
For x² term: - $-6 + 6 = 0$
For x³ term: - $-12 + 16 = 4$

Therefore, the series expansion of f(x) up to the term in x³ is:

$f(x) = -1 - x + 0x^2 + 4x^3 + \cdots$

f(x) = \frac{3x - 1}{(1 - 2x)^2} \\[ |x| < \frac{1}{2} \\ Given that, for x ≠ \frac{1}{2}, \frac{3x - 1}{(1 - 2x)^2} = \frac{A}{(1 - 2x)} + \frac{B}{(1 - 2x)^2}, where A and B are constants, (a) find the values of A and B - Edexcel - A-Level Maths Pure - Question 3 - 2006 - Paper 6

find the values of A and B.

Hence, or otherwise, find the series expansion of f(x), in ascending powers of x, up to and including the term in x³, simplifying each term.

Join the A-Level students using SimpleStudy...