A-Level Edexcel Maths Pure Radian Measure: 5. (a) Given that 5sinθ = 2cosθ,

5. (a) Given that 5sinθ = 2cosθ, find the value of tanθ - Edexcel - A-Level Maths Pure - Question 6 - 2010 - Paper 3

Question 6

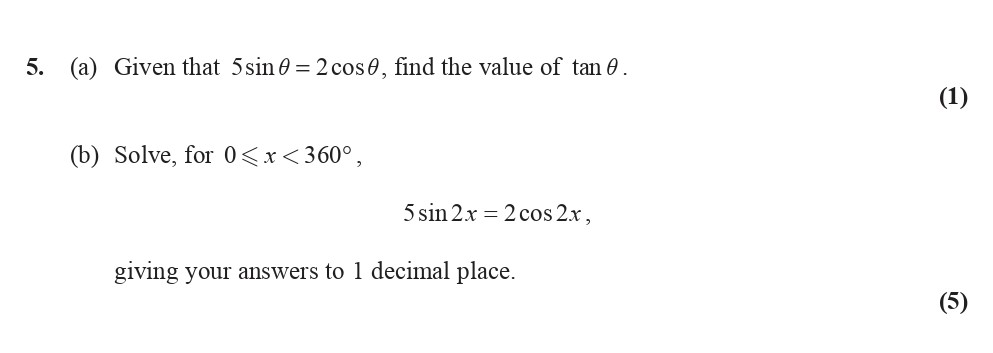
5. (a) Given that 5sinθ = 2cosθ, find the value of tanθ. (b) Solve, for 0 ≤ x < 360°, 5sin2x = 2cos2x, giving your answers to 1 decimal place.

Worked Solution & Example Answer:5. (a) Given that 5sinθ = 2cosθ, find the value of tanθ - Edexcel - A-Level Maths Pure - Question 6 - 2010 - Paper 3

Step 1

96%

114 rated

Answer

To find the value of

$anθ$ ,

we start with the given relationship:

$5 ext{sin}θ = 2 ext{cos}θ$ .

Dividing both sides by

$ext{cos}θ$

(yielding conditions that

eq 0$$): $$5 rac{ ext{sin}θ}{ ext{cos}θ} = 2$$ This simplifies to: $$5 anθ = 2$$ Thus, $$ anθ = rac{2}{5} = 0.4$$.

Step 2

99%

104 rated

Answer

Start with the equation:

$5 ext{sin}(2x) = 2 ext{cos}(2x)$ .

Dividing both sides by

$ext{cos}(2x)$

(assuming

eq 0$$): $$5 an(2x) = 2$$ This gives us: $$ an(2x) = rac{2}{5} = 0.4$$. Next, find the general solutions: $$2x = an^{-1}(0.4) + nπ$$ For $$n = 0$$, we calculate: $$2x = 21.8^ ext{o}$$ which gives: $$x = rac{21.8^ ext{o}}{2} = 10.9^ ext{o}$$. For $$n = 1$$: $$2x = 21.8^ ext{o} + π$$ which corresponds to: $$x = rac{21.8^ ext{o} + 180^ ext{o}}{2} = 100.9^ ext{o}$$. For $$n = 2$$: $$2x = 21.8^ ext{o} + 2π$$ which leads to: $$x = rac{21.8^ ext{o} + 360^ ext{o}}{2} = 180.9^ ext{o}$$. Keep in mind the range for $$x$$ is restricted to $$0 ≤ x < 360^ ext{o}$$. Thus, the answers are: $$x = 10.9^ ext{o}, 100.9^ ext{o}, 180.9^ ext{o}$$. All angles are given to 1 decimal place.