Photo AI
8. (a) By writing sec θ = \frac{1}{\cos θ}, show that \frac{d}{dθ}(sec θ) = sec θ \tan θ (b) Given that x = e^{sec y}, x > e, 0 < y < \frac{\pi}{2} show that \frac{dy}{dx} = \frac{1}{x \cdot g(x)}, \quad x > e where g(x) is a function of \ln x. - Edexcel - A-Level Maths Pure - Question 1 - 2017 - Paper 5
Question 1
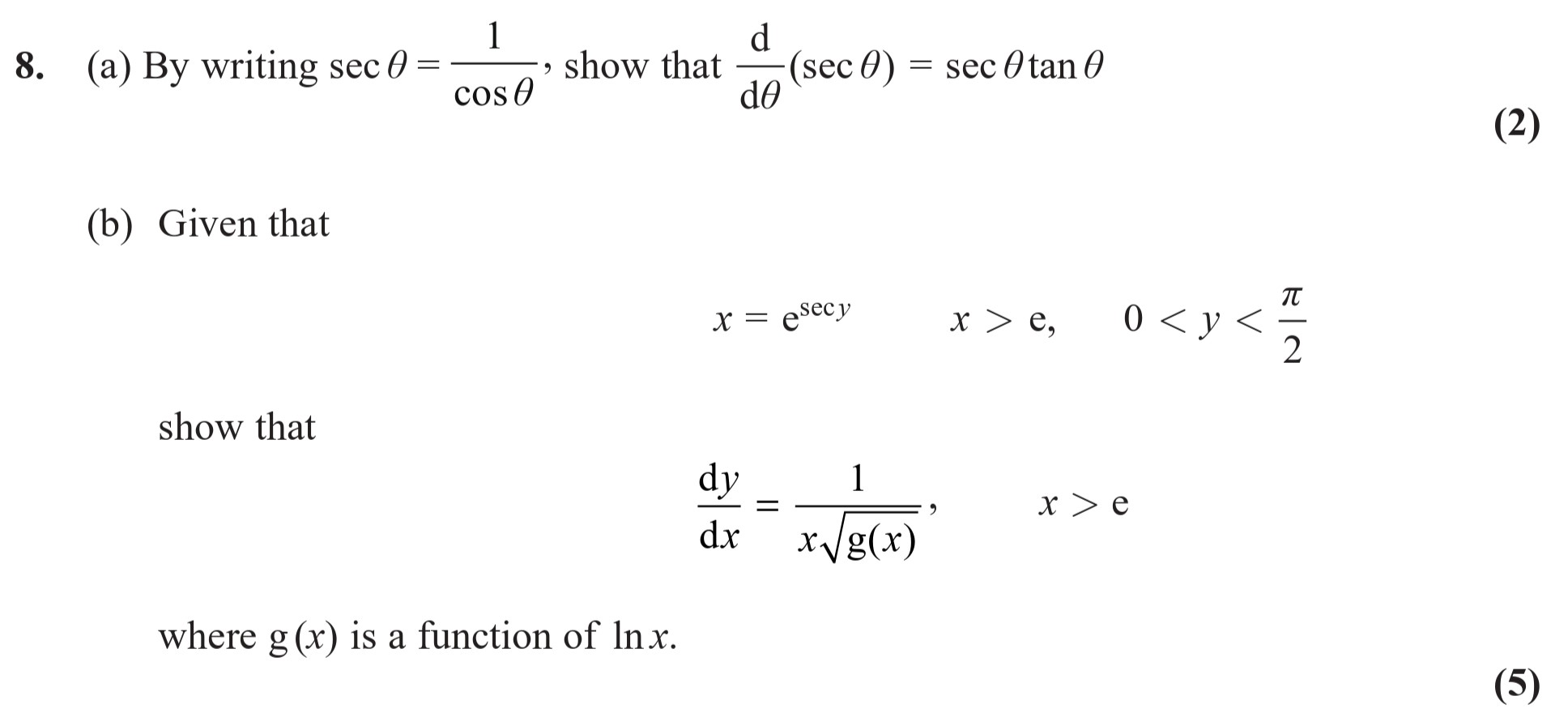
8. (a) By writing sec θ = \frac{1}{\cos θ}, show that \frac{d}{dθ}(sec θ) = sec θ \tan θ (b) Given that x = e^{sec y}, x > e, 0 < y < \frac{\pi}{2} show th... show full transcript
Worked Solution & Example Answer:8. (a) By writing sec θ = \frac{1}{\cos θ}, show that \frac{d}{dθ}(sec θ) = sec θ \tan θ (b) Given that x = e^{sec y}, x > e, 0 < y < \frac{\pi}{2} show that \frac{dy}{dx} = \frac{1}{x \cdot g(x)}, \quad x > e where g(x) is a function of \ln x. - Edexcel - A-Level Maths Pure - Question 1 - 2017 - Paper 5
Step 1
By writing sec θ = \frac{1}{\cos θ}, show that \frac{d}{dθ}(sec θ) = sec θ \tan θ
Answer
To differentiate \sec θ, we start by expressing it as \sec θ = \frac{1}{\cos θ}.
Using the quotient rule for derivatives:
[ \frac{d}{dθ}(\sec θ) = \frac{d}{dθ}\left(\frac{1}{\cos θ}\right) = \frac{0 \cdot \cos θ - (1)(-\sin θ)}{(\cos θ)^2} = \frac{\sin θ}{\cos^2 θ} ] Substituting the identity \sec θ = \frac{1}{\cos θ}, we have:
[ \frac{\sin θ}{\cos^2 θ} = \sec θ \tan θ ]
Step 2
Given that x = e^{sec y}, show that \frac{dy}{dx} = \frac{1}{x \cdot g(x)}, \quad x > e
Answer
Starting with the relationship provided: [ x = e^{\sec y} ]
We differentiate both sides with respect to x:
[
\frac{dx}{dy} = e^{\sec y} \sec y \tan y
]
Thus, we can express the derivative by inverting it:
[
\frac{dy}{dx} = \frac{1}{x \sec y \tan y}
]
Next, we recognize that \sec y = \frac{x}{g(x)} ] where g(x) is a function of \ln x. Therefore, we can rewrite the derivative in terms of g(x):
[
\frac{dy}{dx} = \frac{1}{x \cdot g(x)}
]
This shows the required relationship.
