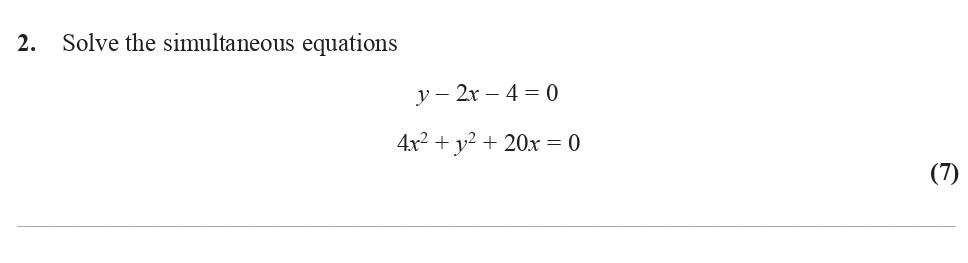Solve the simultaneous equations
$$y - 2x - 4 = 0$$
$$4x^2 + y^2 + 20x = 0$$ - Edexcel - A-Level Maths Pure - Question 4 - 2015 - Paper 1

Question 4
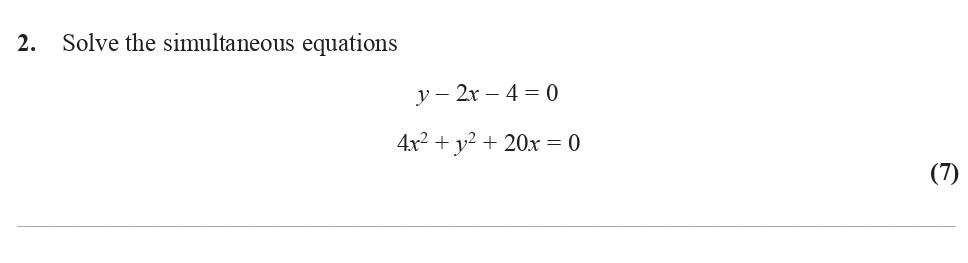
Solve the simultaneous equations
$$y - 2x - 4 = 0$$
$$4x^2 + y^2 + 20x = 0$$
Worked Solution & Example Answer:Solve the simultaneous equations
$$y - 2x - 4 = 0$$
$$4x^2 + y^2 + 20x = 0$$ - Edexcel - A-Level Maths Pure - Question 4 - 2015 - Paper 1
Sub-part a: Solve for y in terms of x

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
From the equation y−2x−4=0, we can express y as:
y=2x+4.
Sub-part b: Substitute into the second equation

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Now substitute y=2x+4 into the second equation:
4x2+(2x+4)2+20x=0.
Expanding the equation:
4x2+(4x2+16x+16)+20x=0
Combine like terms:
8x2+36x+16=0.
Sub-part c: Solve the quadratic equation

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Using the quadratic formula, x=2a−b±b2−4ac, where a=8, b=36, and c=16:
First calculate the discriminant:
b2−4ac=362−4⋅8⋅16=1296−512=784.
Now plug the values into the quadratic formula:
x=2⋅8−36±784=16−36±28.
This gives us two solutions for x:
- x=16−8=−0.5
- x=16−64=−4.
Sub-part d: Find the corresponding y values

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Now, we can find the corresponding values of y for these x values:
- When x=−0.5:
y=2(−0.5)+4=3
- When x=−4:
y=2(−4)+4=−4.
Thus, the solutions to the simultaneous equations are:
- (−0.5,3)
- (−4,−4).
Join the A-Level students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered