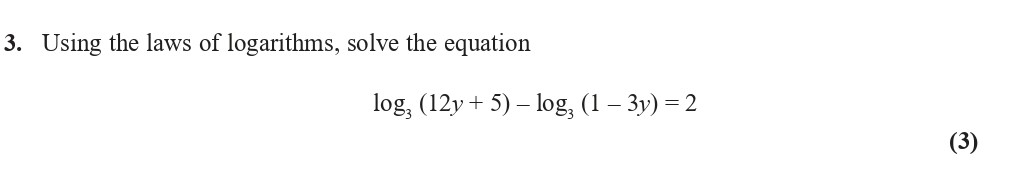Photo AI

Using the laws of logarithms, solve the equation $$\log_3 (12y + 5) - \log_3 (1 - 3y) = 2$$ - Edexcel - A-Level Maths Pure - Question 4 - 2021 - Paper 1

Question icon

Question 4

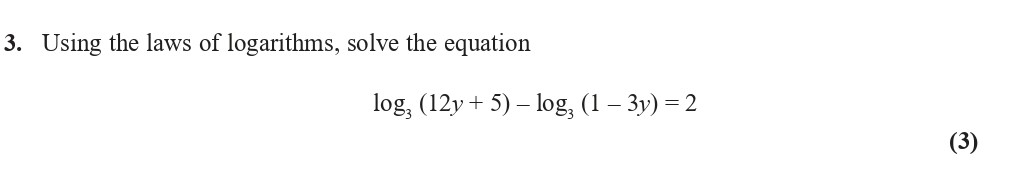
Using-the-laws-of-logarithms,-solve-the-equation--$$\log_3-(12y-+-5)---\log_3-(1---3y)-=-2$$-Edexcel-A-Level Maths Pure-Question 4-2021-Paper 1.png

Using the laws of logarithms, solve the equation $$\log_3 (12y + 5) - \log_3 (1 - 3y) = 2$$

Worked Solution & Example Answer:Using the laws of logarithms, solve the equation $$\log_3 (12y + 5) - \log_3 (1 - 3y) = 2$$ - Edexcel - A-Level Maths Pure - Question 4 - 2021 - Paper 1

Step 1

Step 1: Apply the Laws of Logarithms

96%

114 rated

Answer

Using the property of logarithms: log⁡ab−log⁡ac=log⁡a(bc)\log_a b - \log_a c = \log_a \left( \frac{b}{c} \right) we can rewrite the equation as: log⁡3(12y+51−3y)=2\log_3 \left( \frac{12y + 5}{1 - 3y} \right) = 2

Step 2

Step 2: Exponential Form

99%

104 rated

Answer

Next, we convert the logarithmic equation to its exponential form: 12y+51−3y=32\frac{12y + 5}{1 - 3y} = 3^2 This simplifies to: 12y+51−3y=9\frac{12y + 5}{1 - 3y} = 9

Step 3

Step 3: Cross Multiply

96%

101 rated

Answer

Cross-multiplying gives: 12y+5=9(1−3y)12y + 5 = 9(1 - 3y) Expanding the right-hand side results in: 12y+5=9−27y12y + 5 = 9 - 27y

Step 4

Step 4: Bring Like Terms Together

98%

120 rated

Answer

Now, rearranging the equation we get: 12y+27y=9−512y + 27y = 9 - 5 This simplifies to: 39y=439y = 4

Step 5

Step 5: Solve for y

97%

117 rated

Answer

Finally, divide both sides by 39: y=439y = \frac{4}{39}

Join the A-Level students using SimpleStudy...

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;