Photo AI
Figure 1 shows a sector AOB of a circle with centre O, radius 5 cm and angle AOB = 40° The attempt of a student to find the area of the sector is shown below - Edexcel - A-Level Maths Pure - Question 4 - 2019 - Paper 2
Question 4
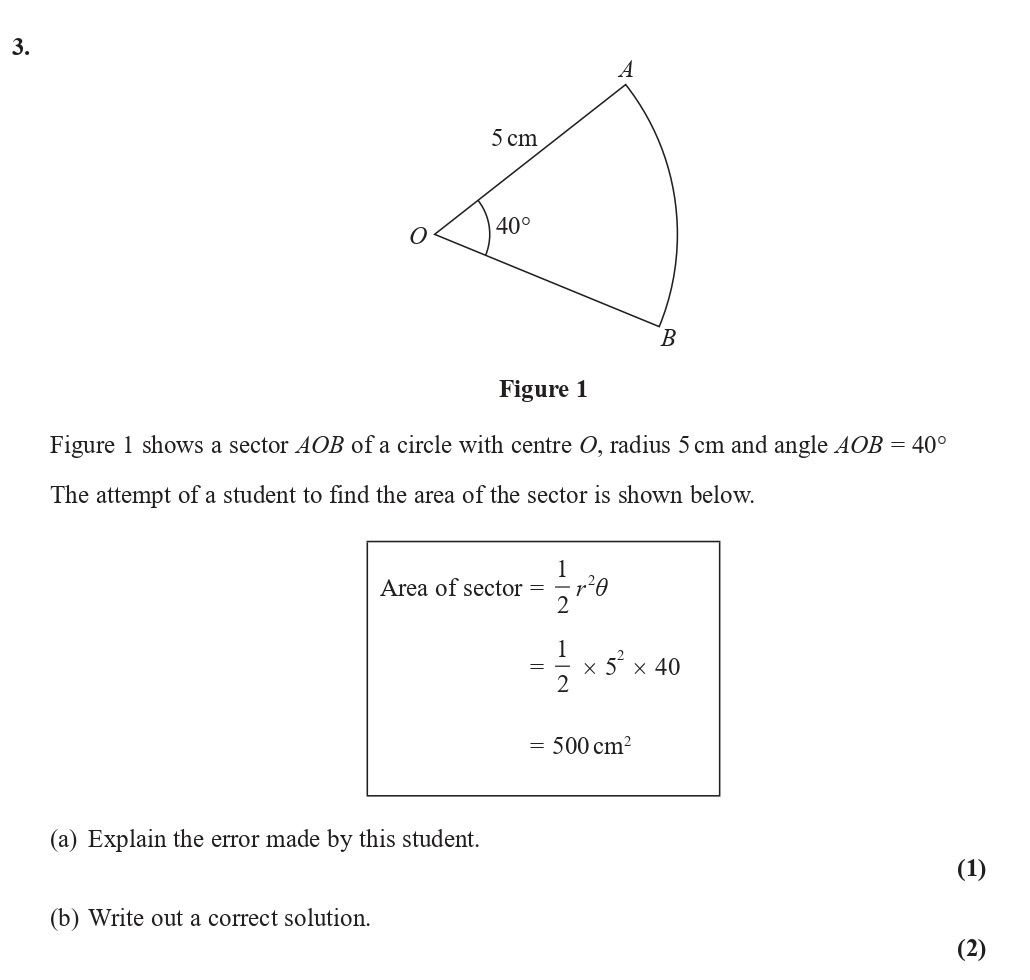
Figure 1 shows a sector AOB of a circle with centre O, radius 5 cm and angle AOB = 40° The attempt of a student to find the area of the sector is shown below. Area ... show full transcript
Worked Solution & Example Answer:Figure 1 shows a sector AOB of a circle with centre O, radius 5 cm and angle AOB = 40° The attempt of a student to find the area of the sector is shown below - Edexcel - A-Level Maths Pure - Question 4 - 2019 - Paper 2
Step 1
(a) Explain the error made by this student.
Answer
The student incorrectly applied the formula for the area of a sector. The error lies in the use of degrees instead of radians for the angle AOB. The angle should be converted to radians before using it in the formula. The correct conversion is given by:
( \theta \text{ (in radians)} = \frac{40 \times \pi}{180} = \frac{2\pi}{9} )
Step 2
(b) Write out a correct solution.
Answer
To find the correct area of the sector, we should use the following formula:
[ \text{Area of sector} = \frac{1}{2} r^2 \theta ]
Substituting the radius and the angle in radians:
[ \text{Area of sector} = \frac{1}{2} \times 5^2 \times \frac{2\pi}{9} = \frac{25\pi}{9} \approx 8.73 \text{ cm}^2 ]
Thus, the area of the sector AOB is approximately 8.73 cm².
