Photo AI
Figure 1 shows a sketch of the graph of $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 8 - 2010 - Paper 2
Question 8
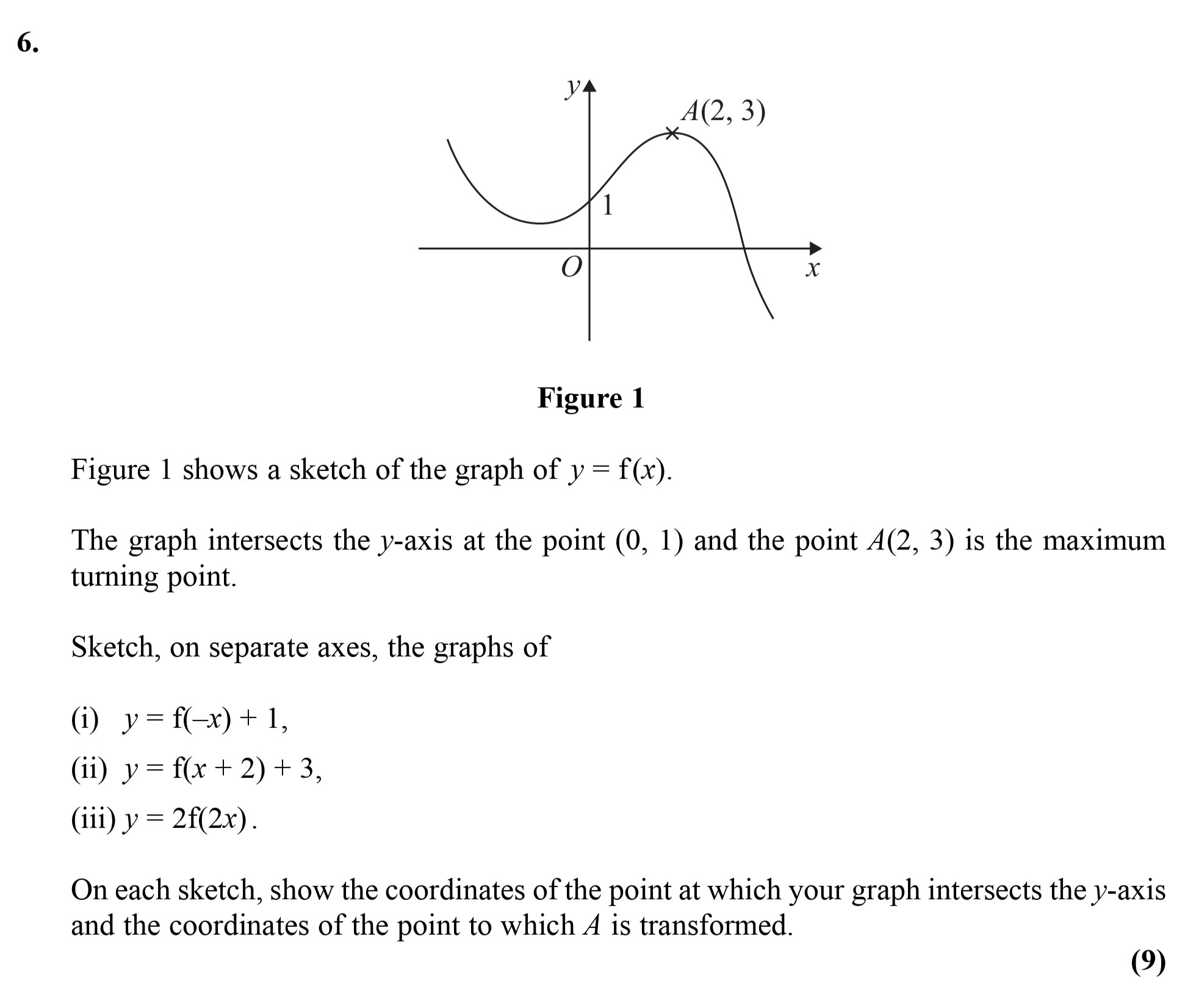
Figure 1 shows a sketch of the graph of $y = f(x)$. The graph intersects the $y$-axis at the point $(0, 1)$ and the point $A(2, 3)$ is the maximum turning point. ... show full transcript
Worked Solution & Example Answer:Figure 1 shows a sketch of the graph of $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 8 - 2010 - Paper 2
Step 1
Step 2
Step 3
