Photo AI
Figure 2 shows a sketch of the curve C with parametric equations $x = ( ad{3}) ext{sin } 2t, \quad y = 4 ext{cos } t, \quad 0 \leq t \leq \pi$ (a) Show that \(\frac{dy}{dx} = k(\sqrt{3})\text{tan } 2t\), where $k$ is a constant to be determined - Edexcel - A-Level Maths Pure - Question 8 - 2012 - Paper 7
Question 8
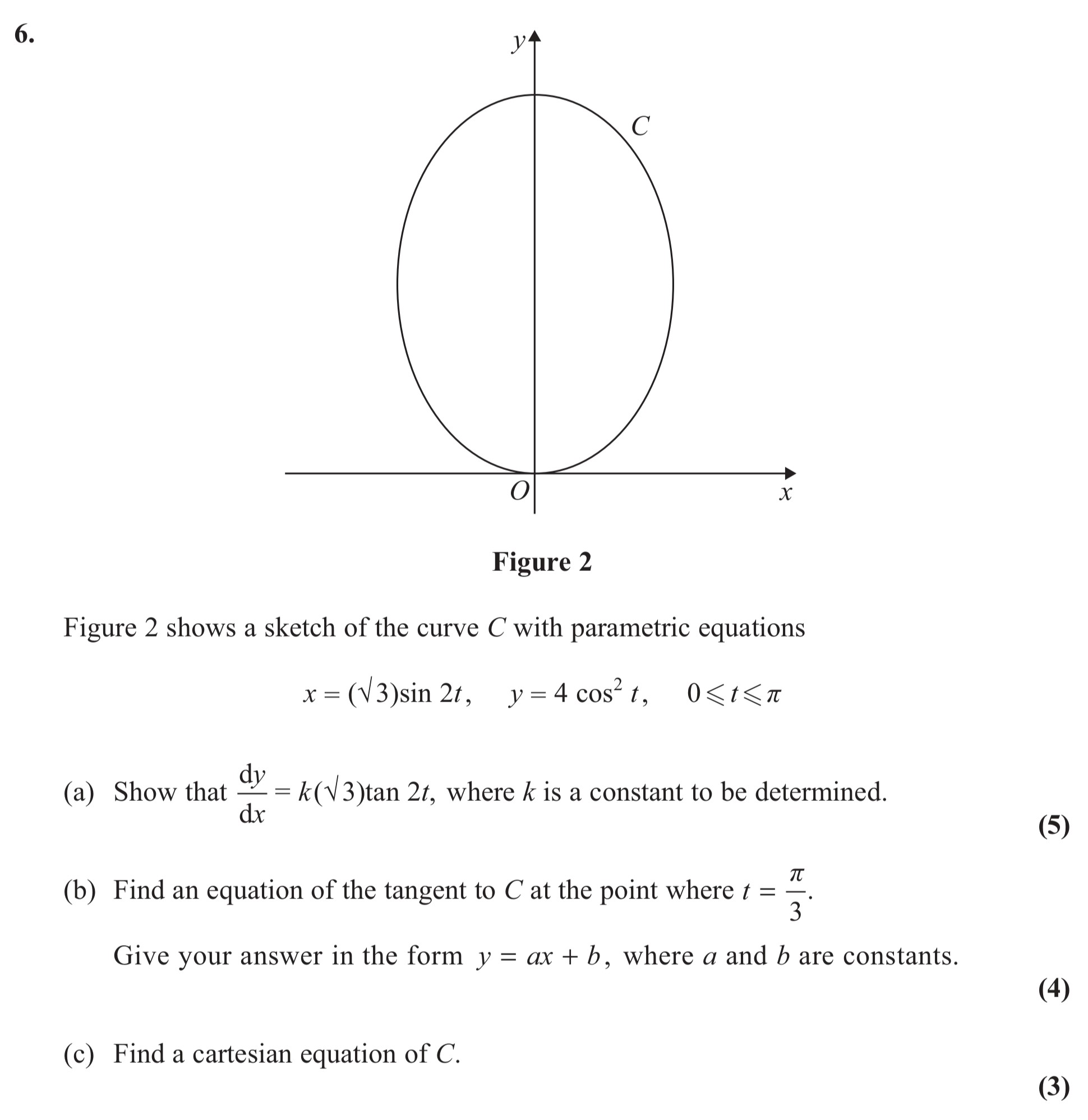
Figure 2 shows a sketch of the curve C with parametric equations $x = ( ad{3}) ext{sin } 2t, \quad y = 4 ext{cos } t, \quad 0 \leq t \leq \pi$ (a) Show that \(\fr... show full transcript
Worked Solution & Example Answer:Figure 2 shows a sketch of the curve C with parametric equations $x = ( ad{3}) ext{sin } 2t, \quad y = 4 ext{cos } t, \quad 0 \leq t \leq \pi$ (a) Show that \(\frac{dy}{dx} = k(\sqrt{3})\text{tan } 2t\), where $k$ is a constant to be determined - Edexcel - A-Level Maths Pure - Question 8 - 2012 - Paper 7
Step 1
Show that \(\frac{dy}{dx} = k(\sqrt{3})\text{tan } 2t\)
Answer
To find (\frac{dy}{dx}), we use the chain rule. First, we calculate (\frac{dx}{dt}) and (\frac{dy}{dt}):
-
Compute (\frac{dx}{dt}):
[ \frac{dx}{dt} = \frac{d}{dt}((\sqrt{3})\text{sin } 2t) = 2\sqrt{3}\text{cos } 2t ] -
Compute (\frac{dy}{dt}):
[ \frac{dy}{dt} = \frac{d}{dt}(4\text{cos } t) = -4\text{sin } t ]
Now calculate (\frac{dy}{dx}):
[ \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{-4\text{sin } t}{2\sqrt{3}\text{cos } 2t} = \frac{-2}{\sqrt{3}} \frac{\text{sin } t}{\text{cos } 2t} ]
Using the double angle identity:
[ \frac{\text{sin } t}{\text{cos } 2t} = \text{tan } 2t ]
Thus:
[ \frac{dy}{dx} = k(\sqrt{3})\text{tan } 2t ] where (k = \frac{-2}{3}) or equivalent constant.
Step 2
Find an equation of the tangent to C at the point where $t = \frac{\pi}{3}$
Answer
-
Substitute into the parametric equations: [ x = (\sqrt{3})\text{sin}(2 \times \frac{\pi}{3}) = (\sqrt{3})\text{sin}(\frac{2\pi}{3}) = (\sqrt{3})\cdot\frac{\sqrt{3}}{2} = \frac{3}{2} ] [ y = 4\text{cos}(\frac{\pi}{3}) = 4 \cdot \frac{1}{2} = 2 ]
-
Find (\frac{dy}{dx}) at this point: [ \frac{dy}{dx} \text{ at } t = \frac{\pi}{3} = k(\sqrt{3})\text{tan}(2 \cdot \frac{\pi}{3}) = k(\sqrt{3})(-\sqrt{3}) = -3 ]
-
The slope of the tangent line is -3. Thus, using point-slope form:
[ y - 2 = -3\left(x - \frac{3}{2}\right) ] -
Rearranging gives:
[ y = -3x + \frac{9}{2} + 2 \Rightarrow y = -3x + \frac{13}{2} ]
Therefore, (a = -3) and (b = \frac{13}{2}).
Step 3
Find a cartesian equation of C
Answer
-
Start with the parametric equations: [ x = (\sqrt{3})\text{sin } 2t, \quad y = 4\text{cos } t ]
-
Solve for (\text{sin } 2t) in terms of (y): [ \text{cos } t = \frac{y}{4} \Rightarrow \text{sin } t = \sqrt{1 - \left(\frac{y}{4}\right)^2} ]
-
Using the double angle formula for sine: [ \text{sin } 2t = 2\text{sin } t \text{cos } t \Rightarrow \text{sin } 2t = 2\sqrt{1 - \left(\frac{y}{4}\right)^2}\cdot\frac{y}{4} ]
-
Substitute into the equation: [ x = \sqrt{3} \cdot 2\cdot\frac{y}{4}\cdot\sqrt{1 - \left(\frac{y}{4}\right)^2} \Rightarrow x = \frac{\sqrt{3}}{2} y \sqrt{1 - \left(\frac{y}{4}\right)^2} ]
-
Square both sides to eliminate the square root and rearrange to find the relation between (x) and (y).
