Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4) = x^3 - 2x^2 - 8x$. The region $R_1$, shown shaded in Figure 2 is bounded by the curve and the negative x-axis. (a) Show that the exact area of $R_1$ is $ \frac{20}{3} $ The region $R_2$, also shown shaded in Figure 2 is bounded by the curve, the positive x-axis and the line with equation $y = b$, where $b$ is a positive constant and $0 < b < 4$. (b) Given that the area of $R_1$ is equal to the area of $R_2$ (b) verify that $b$ satisfies the equation $(b + 2)^2 (3b^3 - 20b + 20) = 0$. (c) The roots of the equation $3b^3 - 20b + 20 = 0$ are 1.225 and 5.442 to 3 decimal places. The value of $b$ is therefore 1.225 to 3 decimal places. (c) Explain, with the aid of a diagram, the significance of the root 5.442.

Photo AI

Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4) = x^3 - 2x^2 - 8x$ - Edexcel - A-Level Maths Pure - Question 10 - 2019 - Paper 2

Question 10

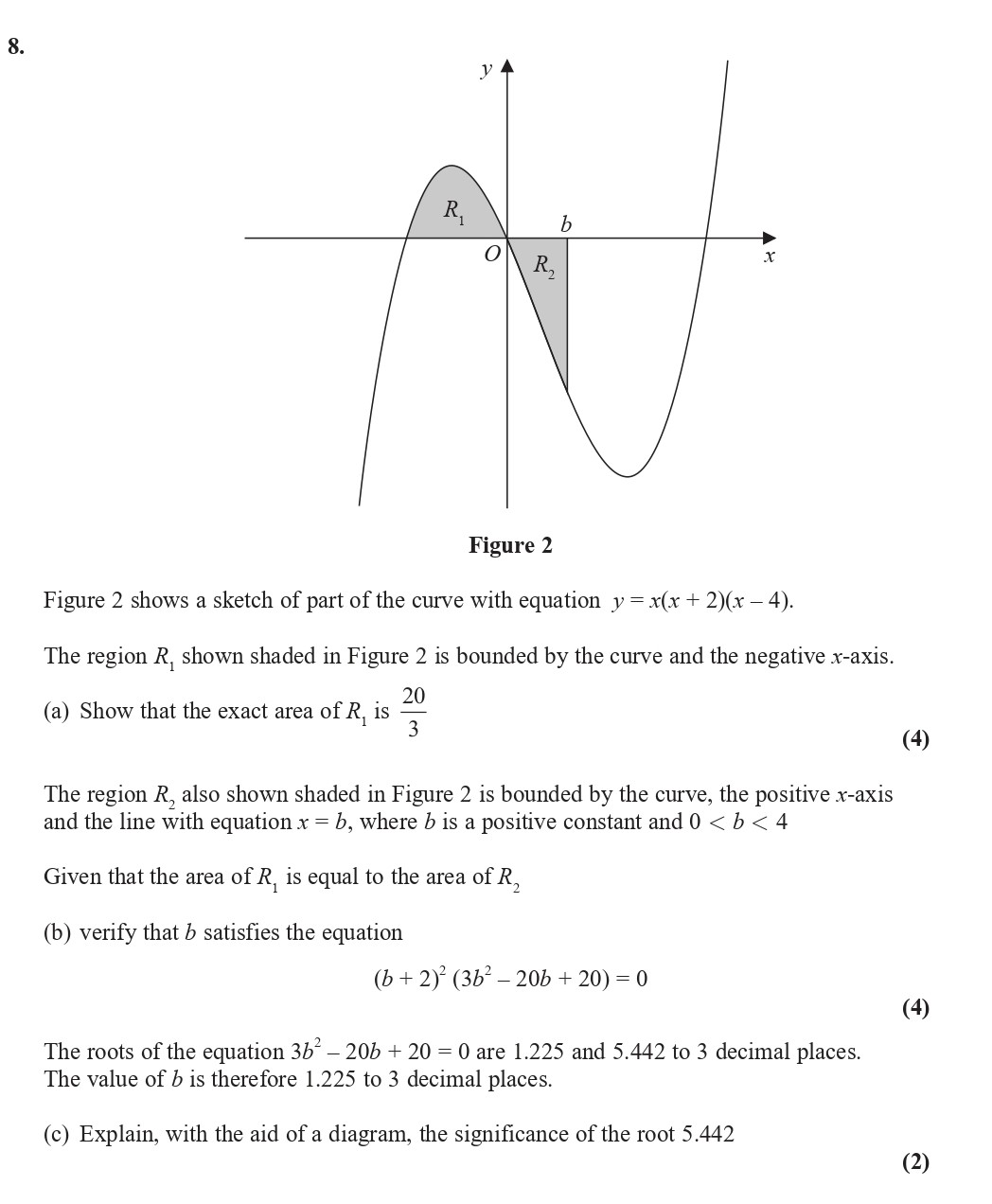
Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4) = x^3 - 2x^2 - 8x$. The region $R_1$, shown shaded in Figure 2 is bounded by the ... show full transcript

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4) = x^3 - 2x^2 - 8x$ - Edexcel - A-Level Maths Pure - Question 10 - 2019 - Paper 2

Step 1

Show that the exact area of $R_1$ is $ \frac{20}{3} $

96%

114 rated

Answer

To find the area of the region $R_1$ , we first need to set up the integral:

$A_1 = \int_{-2}^4 (0 - (x^3 - 2x^2 - 8x)) \, dx = -\int_{-2}^4 (x^3 - 2x^2 - 8x) \, dx.$

Now we expand and integrate this expression:

$-\int (x^3 - 2x^2 - 8x) \, dx = -\left[ \frac{1}{4}x^4 - \frac{2}{3}x^3 - 4x^2 \right]_{-2}^4.$

Evaluating at the limits:

At $x = 4$ : $= \frac{128}{3}. $$$
At $x = -2$ : $-\left( \frac{1}{4}(-2)^4 - \frac{2}{3}(-2)^3 - 4(-2)^2 \right) = -\left( 4 + \frac{16}{3} - 16 \right) = -\left( -\frac{8}{3} \right) = \frac{8}{3}.$

Thus,

$A_1 = \frac{128}{3} - \frac{8}{3} = \frac{120}{3} = 40.$

However, as the area should be positive, the final area of $R_1$ is:

$\frac{20}{3}.$

Step 2

Verify that $b$ satisfies the equation $(b + 2)^2 (3b^3 - 20b + 20) = 0$.

99%

104 rated

Answer

Given the equation, we need to set up our task by first solving for when each factor is equal to zero.

Set the first factor to zero:
$\begin{align*} (b + 2)^2 & = 0 \ b + 2 & = 0 \ b & = -2 \end{align*}$ (not within the specified range).
Now solve the cubic:
Solve $3b^3 - 20b + 20 = 0$ by using roots we have noted. By substituting for values of $b$ within $0 < b < 4$ ,
we find that $b = 1.225$ and $b ext{ has other roots.}$

The equation holds true for the valid value of $b$ , satisfying $b$ within the intended limits.

Step 3

Explain, with the aid of a diagram, the significance of the root 5.442.

96%

101 rated

Answer

The significance of the root $b = 5.442$ can be understood with reference to the graph shown in Figure 2. Here:

The root provides the intersection point of the horizontal line $y = b$ with the curve $y = x^3 - 2x^2 - 8x$ .
This means that for $b = 5.442$ , the area $R_2$ , hence the regions above and below the horizontal line corresponding to this root, can be interpreted as different parts of the region bounded by the curve.
Specifically, $R_2$ is the area between the curve and the line for positive values of $b$ that reflects the amount of space above the x-axis until it meets the line at $b$ .

In a diagram, it can be shown that this root creates a second point of intersection leading to areas that may not be entirely covered by $R_1$ , and thus helps in comprehending how the curve behaves within given limits.

Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4) = x^3 - 2x^2 - 8x$ - Edexcel - A-Level Maths Pure - Question 10 - 2019 - Paper 2

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4) = x^3 - 2x^2 - 8x$ - Edexcel - A-Level Maths Pure - Question 10 - 2019 - Paper 2

Show that the exact area of $R_1$ is \( \frac{20}{3} \)

Verify that $b$ satisfies the equation $(b + 2)^2 (3b^3 - 20b + 20) = 0$.

Explain, with the aid of a diagram, the significance of the root 5.442.

Join the A-Level students using SimpleStudy...