Photo AI
1. The histogram in Figure 1 shows the time, to the nearest minute, that a random sample of 100 motorists were delayed by roadworks on a stretch of motorway - Edexcel - A-Level Maths Statistics - Question 1 - 2012 - Paper 1
Question 1
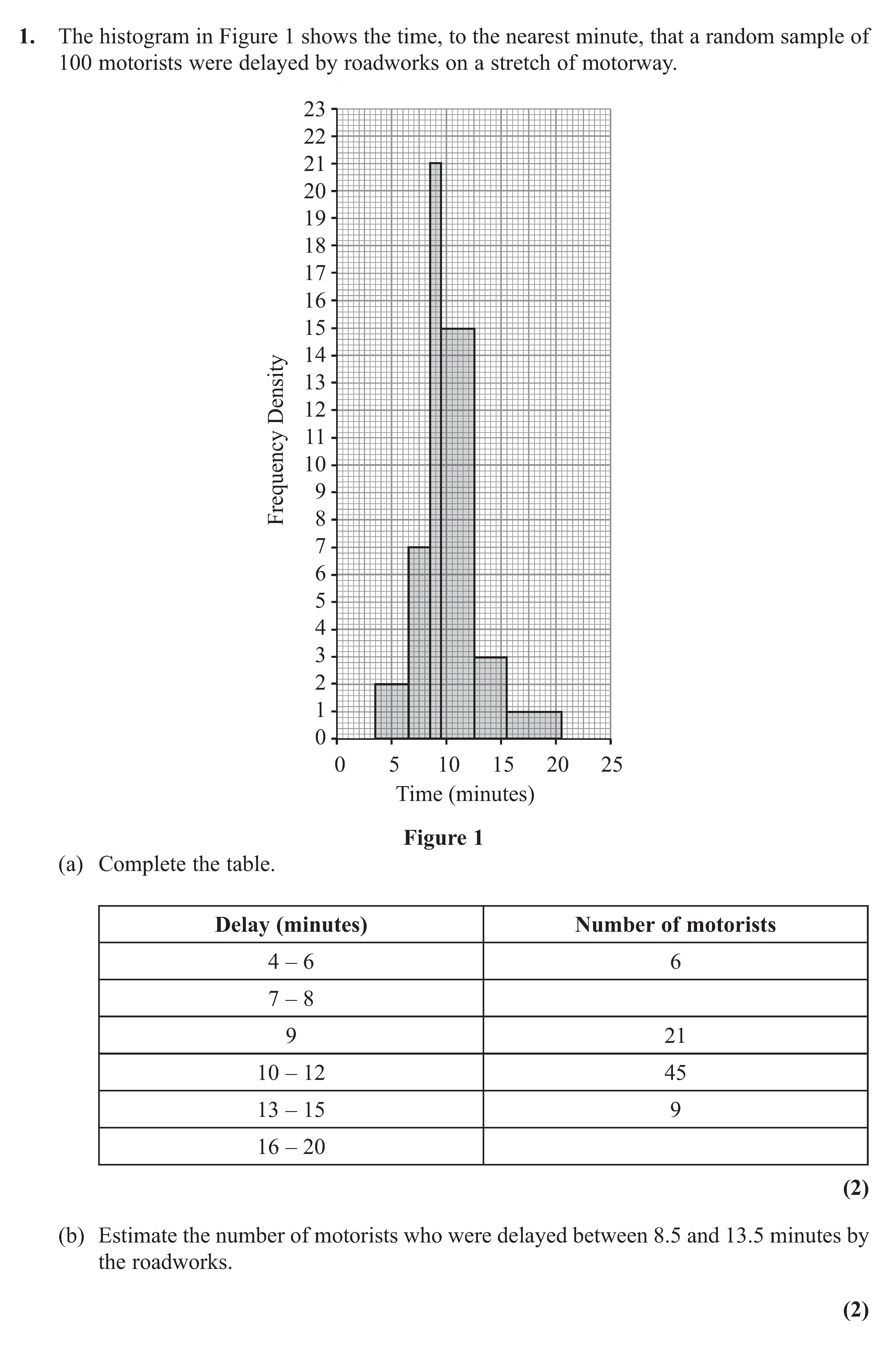
1. The histogram in Figure 1 shows the time, to the nearest minute, that a random sample of 100 motorists were delayed by roadworks on a stretch of motorway. (a) Co... show full transcript
Worked Solution & Example Answer:1. The histogram in Figure 1 shows the time, to the nearest minute, that a random sample of 100 motorists were delayed by roadworks on a stretch of motorway - Edexcel - A-Level Maths Statistics - Question 1 - 2012 - Paper 1
Step 1
Complete the table.
Answer
To complete the table based on the histogram provided in Figure 1:
-
For the delay interval 7 – 8 minutes, we count the number of motorists from the histogram. The frequency density for this interval is about 10, and since this interval represents 1 minute, the number of motorists is:
= 10.
-
For the delay interval 16 – 20 minutes, the frequency is 5. Thus, the number of motorists is:
The completed table is:
| Delay (minutes) | Number of motorists |
|---|---|
| 4 – 6 | 6 |
| 7 – 8 | 10 |
| 9 | 21 |
| 10 – 12 | 45 |
| 13 – 15 | 9 |
| 16 – 20 | 5 |
Step 2
Estimate the number of motorists who were delayed between 8.5 and 13.5 minutes by the roadworks.
Answer
To estimate the number of motorists delayed between 8.5 and 13.5 minutes, we consider:
- From the histogram:
- For the interval 9 minutes, there are 21 motorists.
- For the interval 10 – 12 minutes, there are 45 motorists.
- For the interval 13 – 15 minutes, there are 9 motorists.
Calculating:
- The delay between 8.5 and 9.5 minutes (midpoint) approximately corresponds to 21 motorists.
- The delay from 9.5 to 11.5 minutes (a stretch within 10 – 12 minutes) corresponds to 45 motorists.
- From 11.5 to 13.5 minutes (the upper limit), it can be assumed to be close to half of 9 (which is 4.5 motorists)
To sum up:
ext{Estimated Number} = 21 (8.5 to 9.5) + 45 (9.5 to 11.5) + 4.5 (11.5 to 13.5) = 70.5
Thus, the estimated number of motorists delayed between 8.5 and 13.5 minutes is approximately 69.
