GCSE Edexcel Maths Algebraic Proof: n is an integer. Prove algebrai

n is an integer - Edexcel - GCSE Maths - Question 17 - 2017 - Paper 1

Question 17

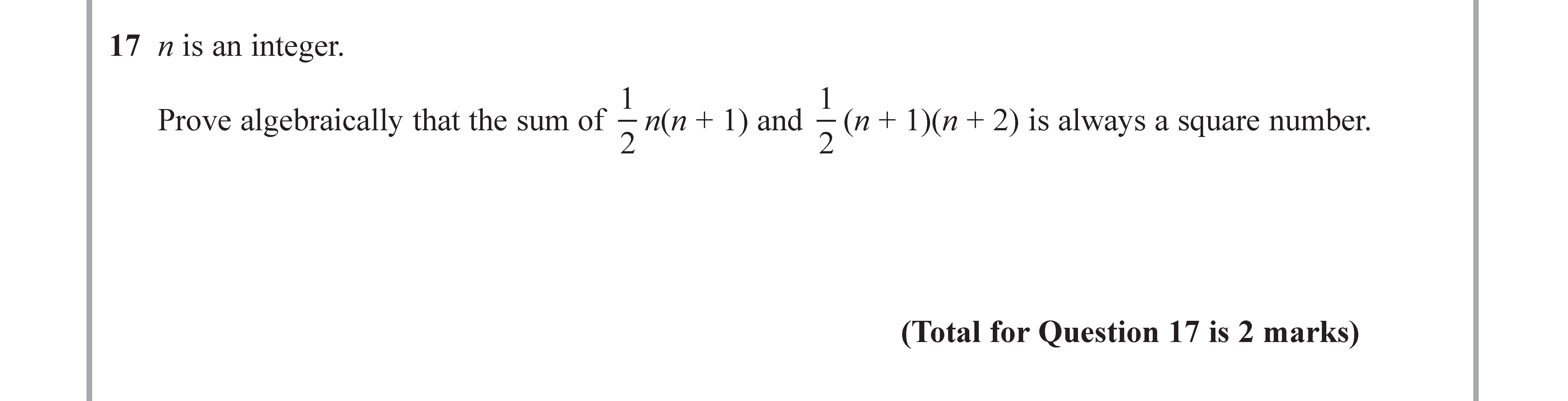
n is an integer. Prove algebraically that the sum of \( \frac{1}{2}n(n + 1) \) and \( \frac{1}{2}(n + 1)(n + 2) \) is always a square number.

Worked Solution & Example Answer:n is an integer - Edexcel - GCSE Maths - Question 17 - 2017 - Paper 1

Step 1

96%

114 rated

Answer

To prove that the sum of ( \frac{1}{2}n(n + 1) ) and ( \frac{1}{2}(n + 1)(n + 2) ) is a square number, we first simplify each term separately:

For ( \frac{1}{2}n(n + 1) ), we can expand this as:

[ \frac{1}{2}n(n + 1) = \frac{1}{2}(n^2 + n) ]
For ( \frac{1}{2}(n + 1)(n + 2) ), we expand:

[ \frac{1}{2}(n + 1)(n + 2) = \frac{1}{2}(n^2 + 3n + 2) ]

Now we can add these two expressions together:

[ \frac{1}{2}(n^2 + n) + \frac{1}{2}(n^2 + 3n + 2) = \frac{1}{2}(2n^2 + 4n + 2) = n^2 + 2n + 1 = (n + 1)^2 ]

Step 2

99%

104 rated

Answer

Thus, we have shown that:

[ \frac{1}{2}n(n + 1) + \frac{1}{2}(n + 1)(n + 2) = (n + 1)^2 ]

Since ( (n + 1)^2 ) is a square number for any integer ( n ), this proves that the sum is always a square number.