Photo AI
The diagram shows three circles, each of radius 4 cm - Edexcel - GCSE Maths - Question 1 - 2022 - Paper 2
Question 1
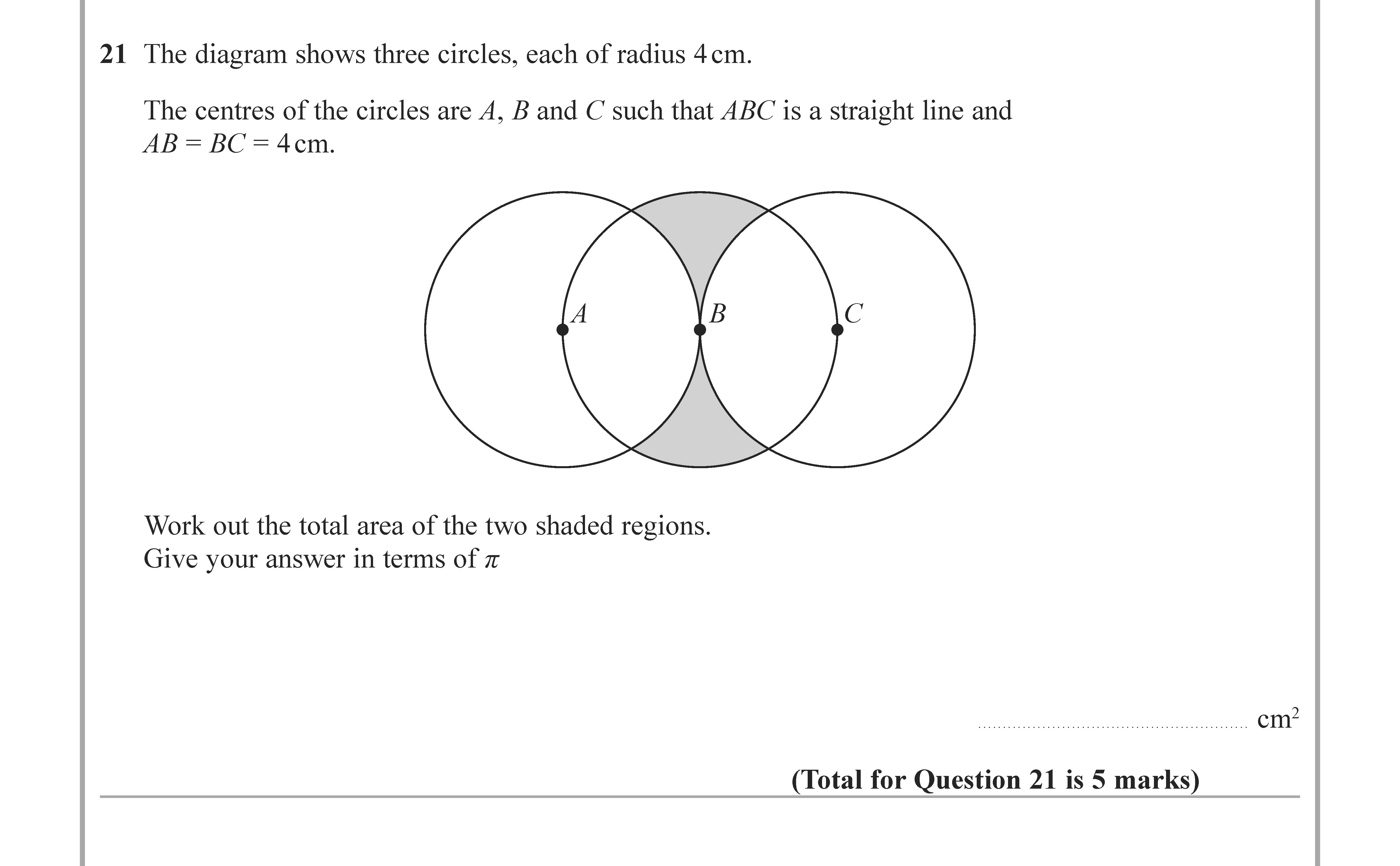
The diagram shows three circles, each of radius 4 cm. The centres of the circles are A, B and C such that ABC is a straight line and AB = BC = 4 cm. Work out the t... show full transcript
Worked Solution & Example Answer:The diagram shows three circles, each of radius 4 cm - Edexcel - GCSE Maths - Question 1 - 2022 - Paper 2
Step 1
Find the area of the segment (for circle A)
Answer
To find the area of one shaded segment in circle A, we first need to determine the angle of the sector formed at center A. Since AB = BC = 4 cm and the radius of the circles is also 4 cm, triangle ABC is isosceles with sides AB and AC equal. The angle at A can be found using the cosine rule or recognizing symmetry.
The angle at A is 120 degrees (as angle B is formed by the two radii).
The area of the sector of circle A can be calculated as:
Next, we find the area of triangle ABC:
For triangle ABC, the height can be calculated by using trigonometry, which gives the height as:
Thus, the area of triangle ABC is:
Therefore, the area of the shaded segment in circle A is:
Step 2
Find the area of the segment (for circle C)
Answer
Using the same approach for circle C, we again have an angle of 120 degrees at center C.
Thus, the area of the sector in circle C is equal to that of circle A:
And the area of triangle ABC remains unchanged:
The area of the shaded segment in circle C is also:
Step 3
