GCSE Edexcel Maths Algebraic Roots & Indices: DEF is a triangle. P is the mid

DEF is a triangle - Edexcel - GCSE Maths - Question 22 - 2020 - Paper 1

Question 22

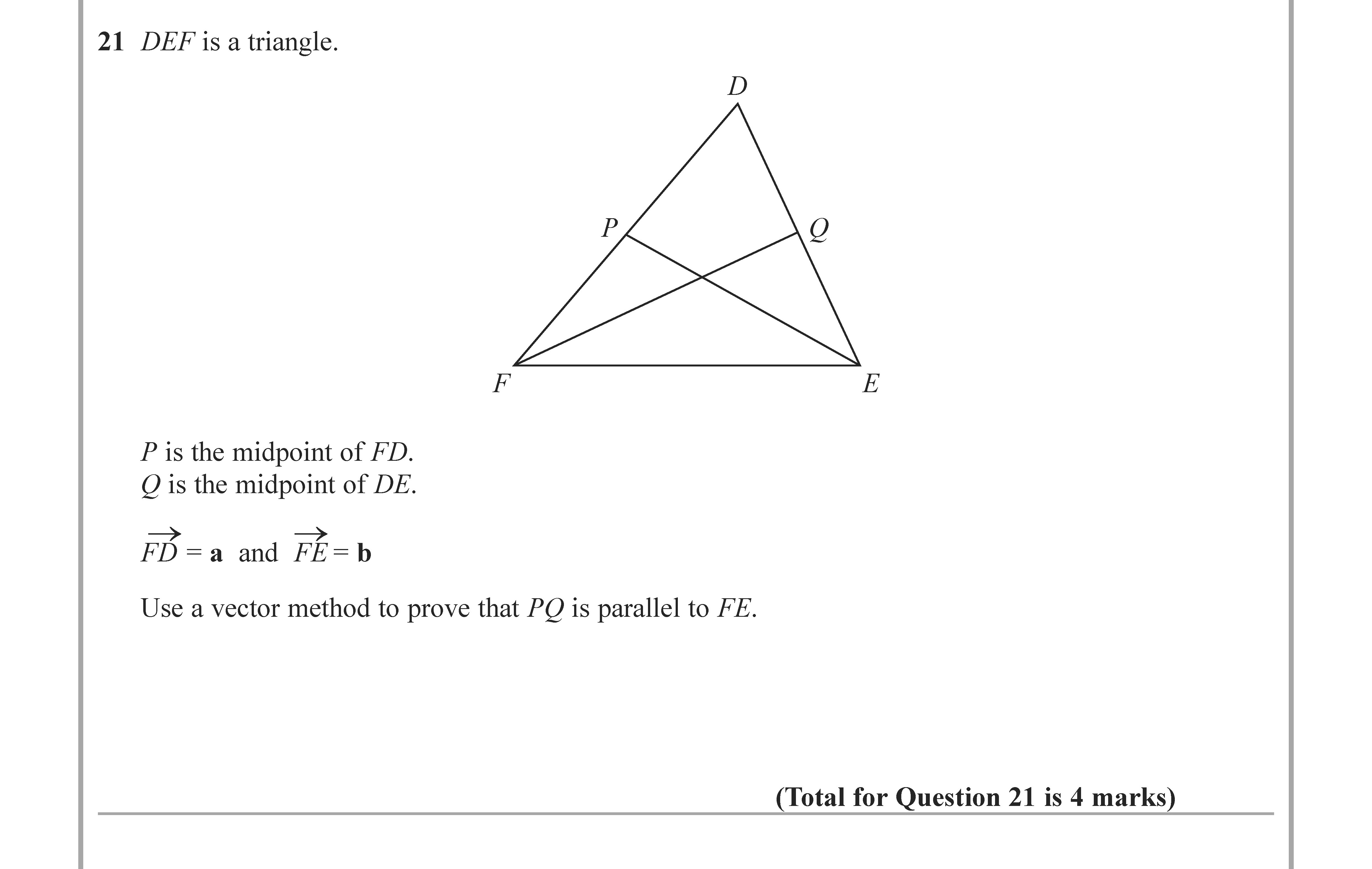
DEF is a triangle. P is the midpoint of FD. Q is the midpoint of DE. → FD = a and → FE = b Use a vector method to prove that PQ is parallel to FE.

Worked Solution & Example Answer:DEF is a triangle - Edexcel - GCSE Maths - Question 22 - 2020 - Paper 1

Step 1

96%

114 rated

Answer

Since P and Q are midpoints, we can express the vector PQ in terms of the given vectors.

We can start by finding the position vectors:

ightarrow{P} = rac{1}{2} ightarrow{F} + rac{1}{2} ightarrow{D}$$ and

ightarrow{Q} = rac{1}{2} ightarrow{D} + rac{1}{2} ightarrow{E}$$.

Now, calculating the vector PQ:

ightarrow{PQ} = ightarrow{Q} - ightarrow{P} = \left(\frac{1}{2} \rightarrow{D} + \frac{1}{2} \rightarrow{E}\right) - \left(\frac{1}{2} \rightarrow{F} + \frac{1}{2} \rightarrow{D}\right) = \frac{1}{2}(\rightarrow{E} - \rightarrow{F}).$$

Step 2

99%

104 rated

Answer

Since we have the vector for PQ calculated, we can relate it back to the vector FE. Based on the stated vectors:

ightarrow{FE} = \rightarrow{E} - \rightarrow{F} = b$$, Thus, $$\rightarrow{PQ} = \frac{1}{2} \rightarrow{FE}.$$

Step 3

96%

101 rated

Answer

The vector PQ is expressed as:

$\rightarrow{PQ} = \frac{1}{2} (\rightarrow{FE})$ .

This shows that PQ is a scalar multiple of FE, thus proving that PQ is parallel to FE.