The diagram shows triangle ABC - Edexcel - GCSE Maths - Question 19 - 2019 - Paper 3
Question 19
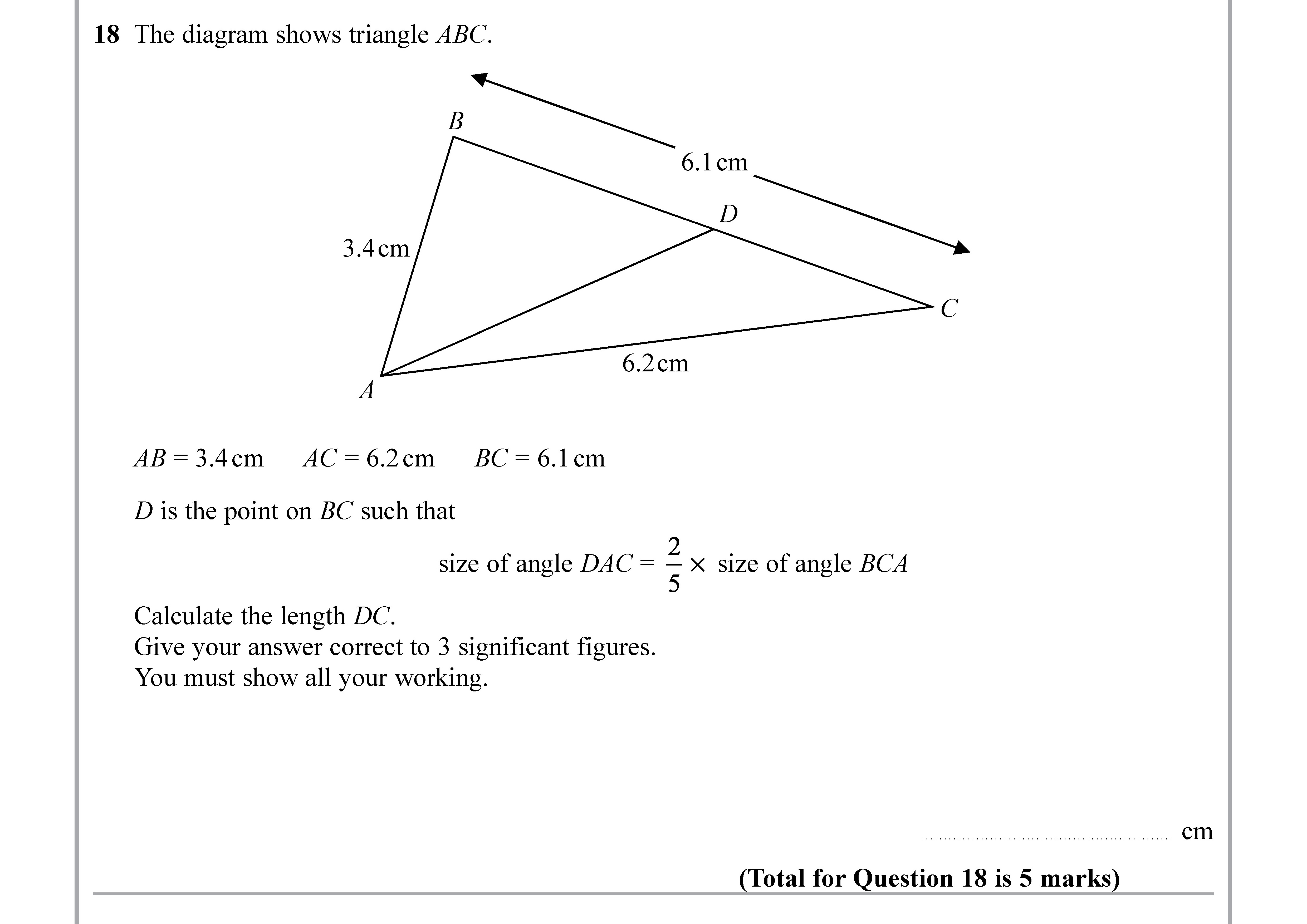
The diagram shows triangle ABC.
AB = 3.4 cm
AC = 6.2 cm
BC = 6.1 cm
D is the point on BC such that size of angle DAC = \frac{2}{5} \text{ size of angle BCA}
Calcu... show full transcript
Worked Solution & Example Answer:The diagram shows triangle ABC - Edexcel - GCSE Maths - Question 19 - 2019 - Paper 3
Step 1
Calculate angle BCA
96%
114 rated
Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Answer
To find angle BCA, we can use the sine rule in triangle ABC:
sin(∠ACB)AB=sin(∠ABC)AC
Let ( \angle BCA ) = ( x ), so ( \angle DAC = \frac{2}{5} x ).
Using the sine rule for the triangle ABC:
sin(x)3.4=sin(∠ABC)6.2
We need to solve for angle x using the known side lengths. We find angle ABC first.
Step 2
Find the size of angle DAC
99%
104 rated
Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Answer
From the relationship we established:
∠DAC=52∠BCA
Therefore, once we find ( x ), we can compute ( \angle DAC ). Let’s find the values.
Step 3
Use the sine rule in triangle ADC
96%
101 rated
Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Answer
For triangle ADC, we can again apply the sine rule:
sin(∠DAC)AC=sin(∠ACD)DC
Where ( DC ) is what we are trying to find, and ( \angle ACD = 180 - (\angle DAC + \angle ABC) $$. We can substitute the known values to find ( DC ).
Step 4
Calculate length DC
98%
120 rated
Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Answer
After substituting the values through sine rule, we arrive at:
DC=sin(∠DAC)6.2⋅sin(∠ACD)
Substituting the values gives us the result. Make sure to round to three significant figures.
