Photo AI
The diagram shows two shaded shapes, A and B - Edexcel - GCSE Maths - Question 23 - 2020 - Paper 1
Question 23
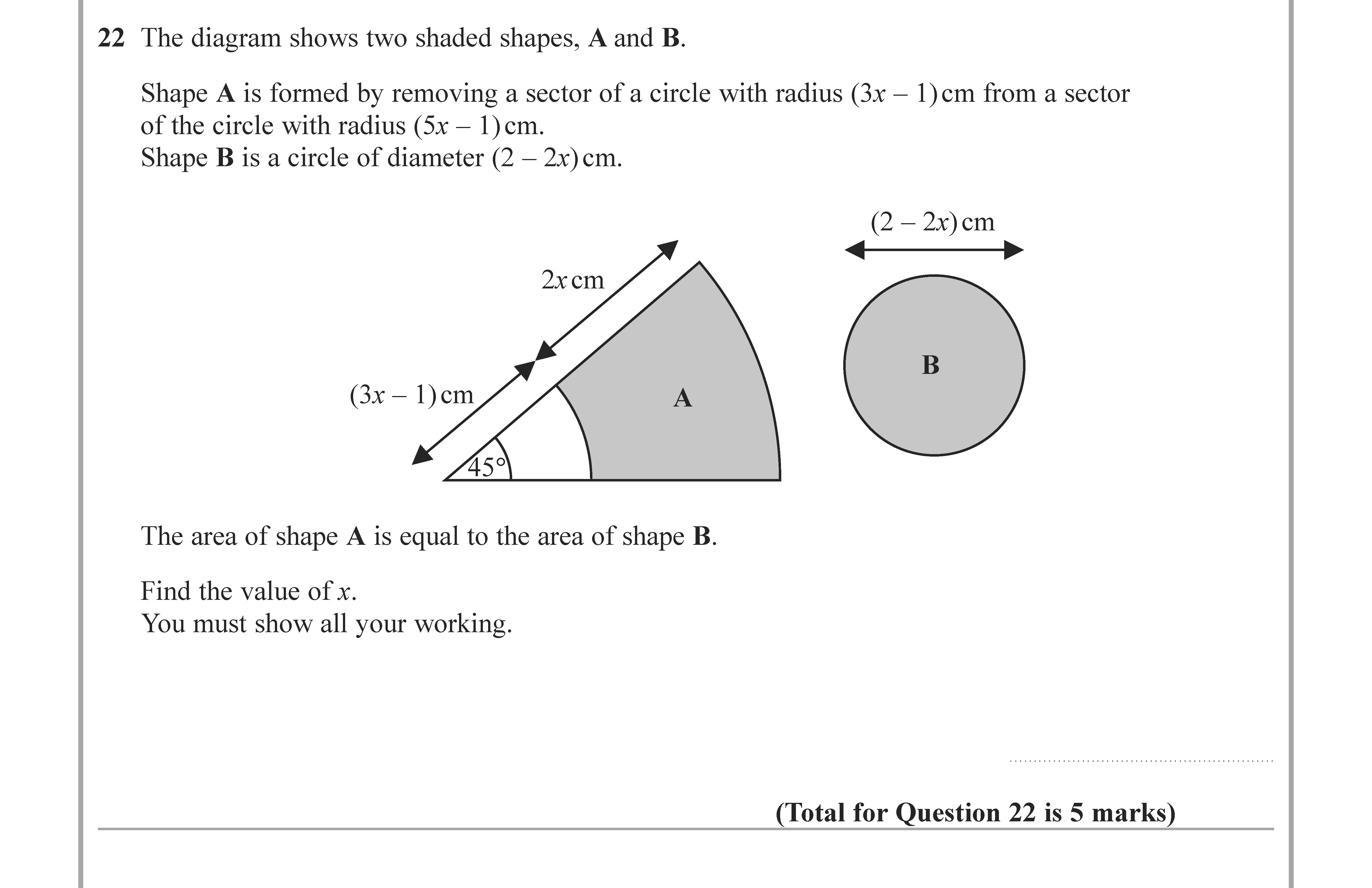
The diagram shows two shaded shapes, A and B. Shape A is formed by removing a sector of a circle with radius $(3x - 1)$ cm from a sector of the circle with radius $... show full transcript
Worked Solution & Example Answer:The diagram shows two shaded shapes, A and B - Edexcel - GCSE Maths - Question 23 - 2020 - Paper 1
Step 1
Derive an algebraic expression for the area of A
Answer
To find the area of shape A, we first find the area of the sector with radius cm and the sector with radius cm.
The formula for the area of a sector is given by:
The angle for both sectors is the same, let's denote it as . Hence, the area of shape A becomes:
This simplifies to:
Step 2
Step 3
Step 4
Factor or use the quadratic formula
Answer
At this point, we can either factor the quadratic or apply the quadratic formula:
Substituting the coefficients obtained from the quadratic equation will give us the values for . Upon solving, we can deduce the value of that satisfies the area equality.
