CDEF is a quadrilateral - Edexcel - GCSE Maths - Question 1 - 2019 - Paper 2

Question 1
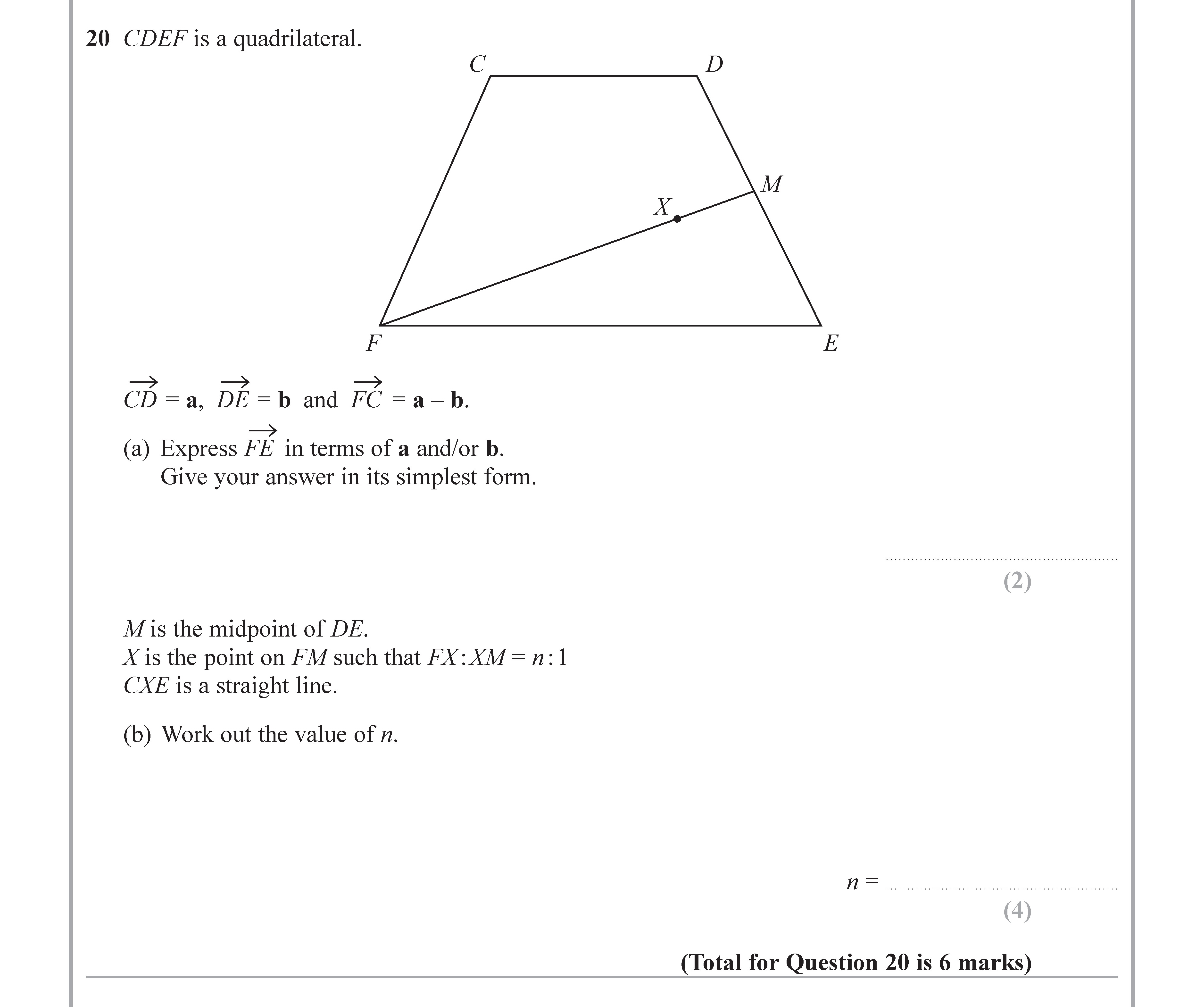
CDEF is a quadrilateral.
$$ \vec{CD} = \mathbf{a}, \quad \vec{DE} = \mathbf{b} \quad \text{and} \quad \vec{CF} = \mathbf{a} - \mathbf{b}. $$
(a) Express $\vec{FE}$... show full transcript
Worked Solution & Example Answer:CDEF is a quadrilateral - Edexcel - GCSE Maths - Question 1 - 2019 - Paper 2
Express $\vec{FE}$ in terms of $\mathbf{a}$ and $\mathbf{b}$

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To express FE, we can use the relationships between the vectors provided. We know that:
-
Start from point F:
We can express F in terms of C and DE:
F=C+CF=C+(a−b).
-
Next, we find E in terms of D and DE:
E=D+DE=C+a+b.
-
Using these expressions, we can find FE:
FE=E−F=(C+a+b)−(C+(a−b)).
Simplifying this, we get:
FE=b+b=2b.
Work out the value of n

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Given that M is the midpoint of DE and X is the point on FM such that FX:XM=n:1 and CVE is a straight line:
-
Since M is the midpoint, we can express:
M=2D+E.
Substituting for D and E:
M=2(C+a)+(C+a+b)=C+a+2b.
-
Now, we can express X on line FM:
X=n+1nF+n+11M.
-
Using the conditions for collinearity of C,V,E, we can find n. By equating the ratios of segments, we derive:
n+1=2 (from balance of weights),
yielding:
n=1.
Join the GCSE students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered

