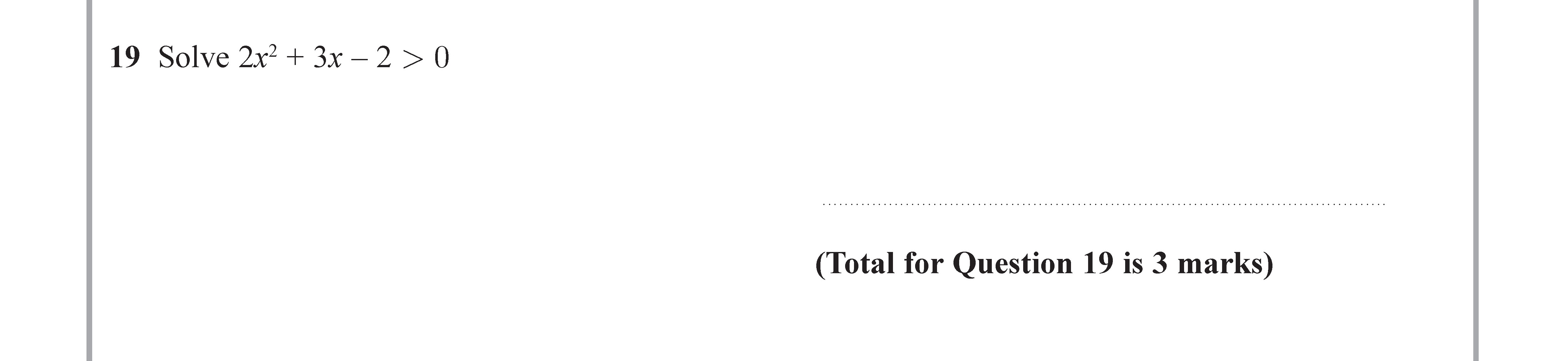Solve 2x² + 3x - 2 > 0
- Edexcel - GCSE Maths - Question 19 - 2017 - Paper 3

Question 19
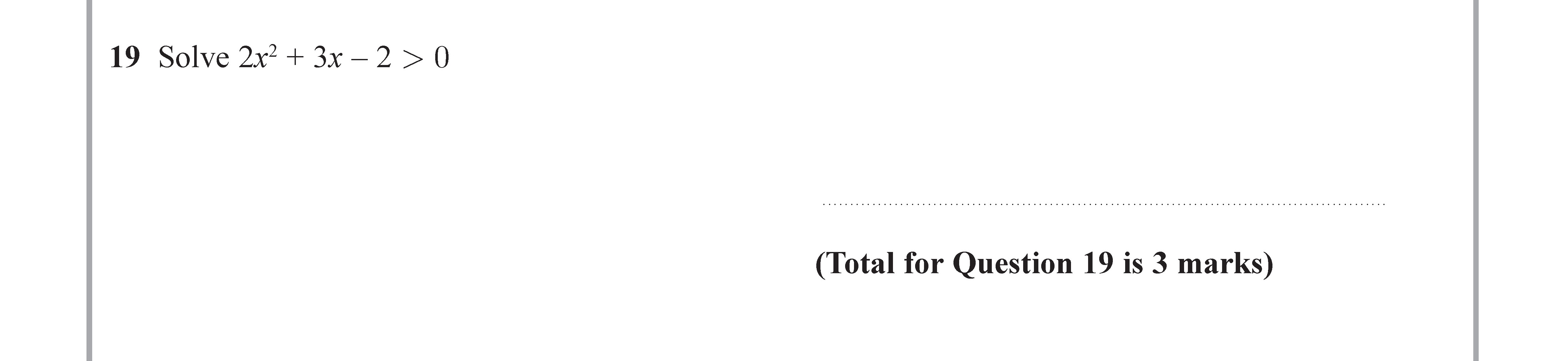
Solve 2x² + 3x - 2 > 0
Worked Solution & Example Answer:Solve 2x² + 3x - 2 > 0
- Edexcel - GCSE Maths - Question 19 - 2017 - Paper 3
Factor the quadratic equation

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To solve the inequality, we start by factoring the quadratic expression on the left side:
2x2+3x−2=0
We can factor this as follows:
(2x−1)(x+2)=0
Find the roots of the equation

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Setting each factor to zero, we find the roots:
- 2x−1=0⟹x=21
- x+2=0⟹x=−2
Determine the intervals

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
The x-values that make the expression zero are x=−2 and x=21. These roots divide the number line into three intervals:
- (−∞,−2)
- (−2,21)
- (21,∞)
Test values in each interval

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
We test a value from each interval in the inequality 2x2+3x−2>0:
-
For x=−3 (from (−∞,−2)):
2(−3)2+3(−3)−2=18−9−2=7>0
-
For x=0 (from (−2,21)):
2(0)2+3(0)−2=−2<0
-
For x=1 (from (21,∞)):
2(1)2+3(1)−2=2+3−2=3>0
Conclusion

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
The expression is greater than zero in the intervals (−∞,−2) and (21,∞). Therefore, the solution is:
x<−2orx>21
Join the GCSE students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered