Photo AI
ABC is a triangle - Edexcel - GCSE Maths - Question 1 - 2021 - Paper 1
Question 1
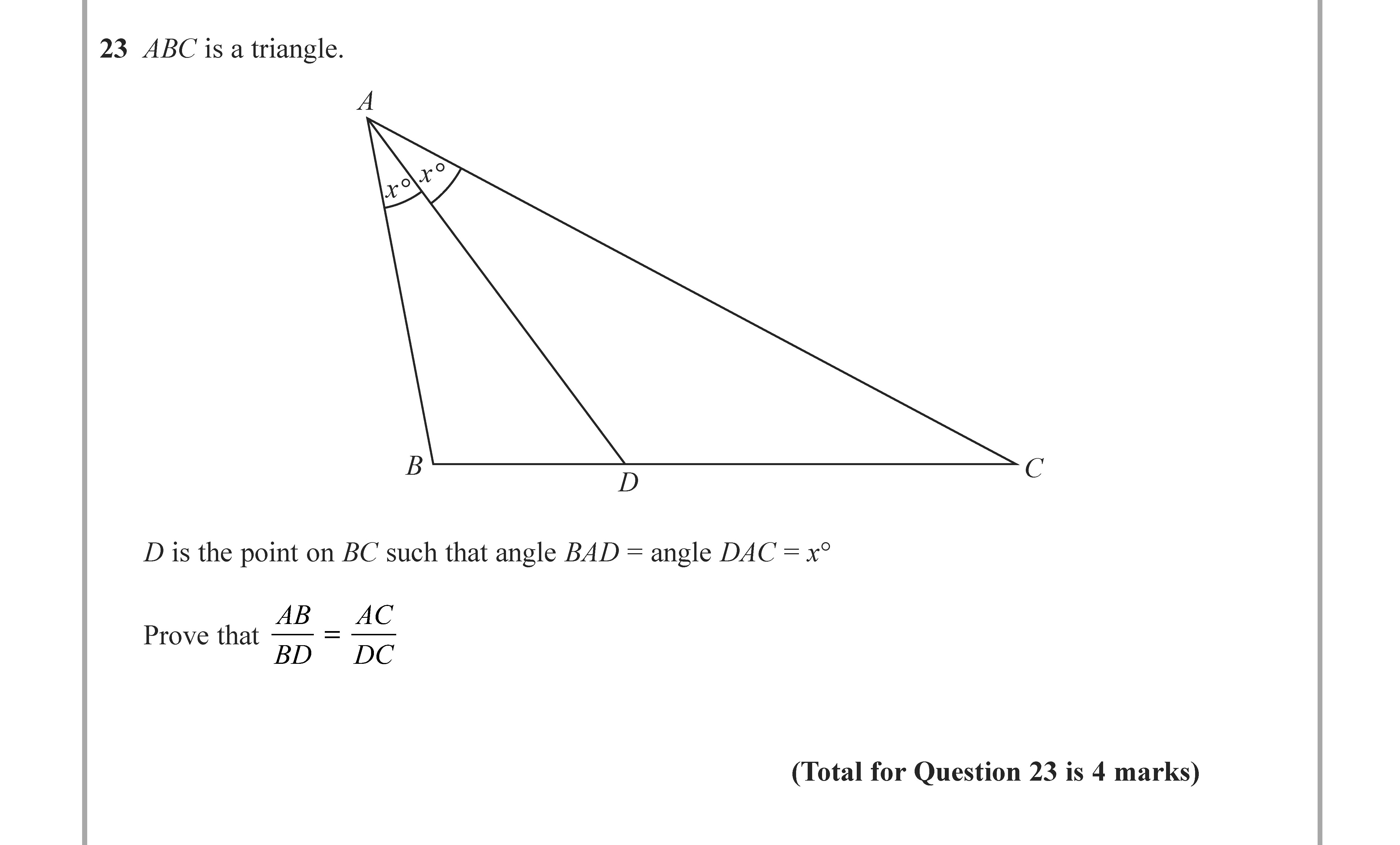
ABC is a triangle. D is the point on BC such that angle BAD = angle DAC = -y°. Prove that AB/BD = AC/DC.
Worked Solution & Example Answer:ABC is a triangle - Edexcel - GCSE Maths - Question 1 - 2021 - Paper 1
Step 1
Step 2
Step 3
