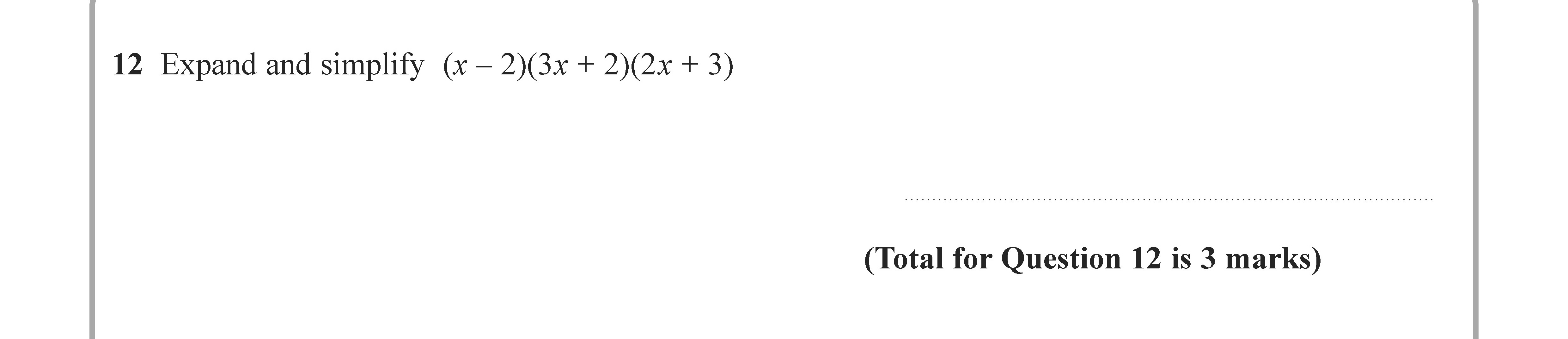Expand and simplify $(x - 2)(x^2 + 2x + 3)$
(Total for Question 12 is 3 marks) - Edexcel - GCSE Maths - Question 13 - 2021 - Paper 2

Question 13
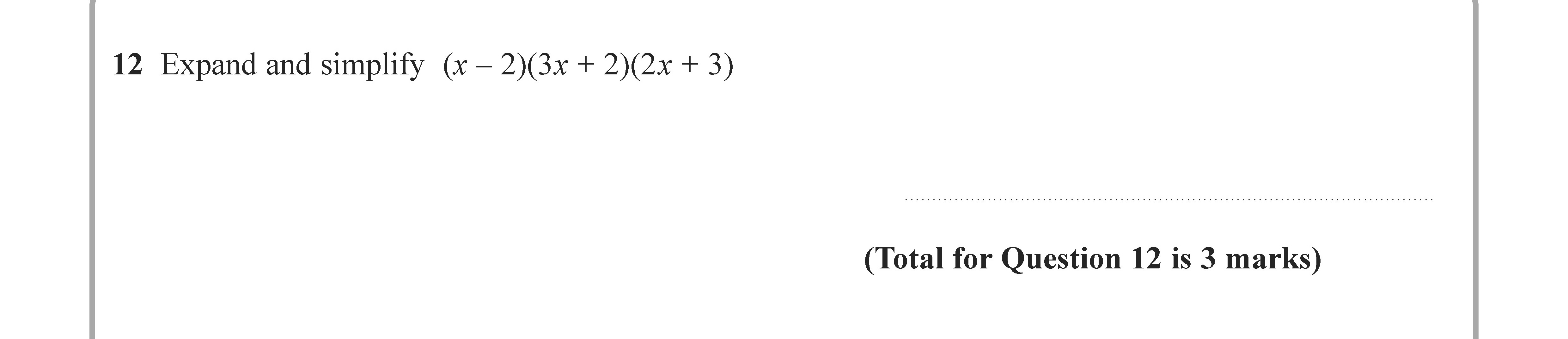
Expand and simplify $(x - 2)(x^2 + 2x + 3)$
(Total for Question 12 is 3 marks)
Worked Solution & Example Answer:Expand and simplify $(x - 2)(x^2 + 2x + 3)$
(Total for Question 12 is 3 marks) - Edexcel - GCSE Maths - Question 13 - 2021 - Paper 2
Expand the expression

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To expand the expression, we apply the distributive property (also known as the FOIL method for binomials).
the expression can be expanded as follows:
(x−2)(x2+2x+3)=x(x2+2x+3)−2(x2+2x+3)
Calculating each part:
-
For the first term:
x(x2+2x+3)=x3+2x2+3x
-
For the second term:
−2(x2+2x+3)=−2x2−4x−6
Now we combine these results:
x3+2x2+3x−2x2−4x−6.
Combine like terms

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Now we simplify by combining like terms:
- The x2 terms: ( 2x^2 - 2x^2 = 0 )
- The x terms: ( 3x - 4x = -x )
- The constant term remains: ( -6 )
Thus, the simplified expression is:
x3−x−6Join the GCSE students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered