Photo AI

OAB is a triangle - Edexcel - GCSE Maths - Question 22 - 2018 - Paper 1

Question icon

Question 22

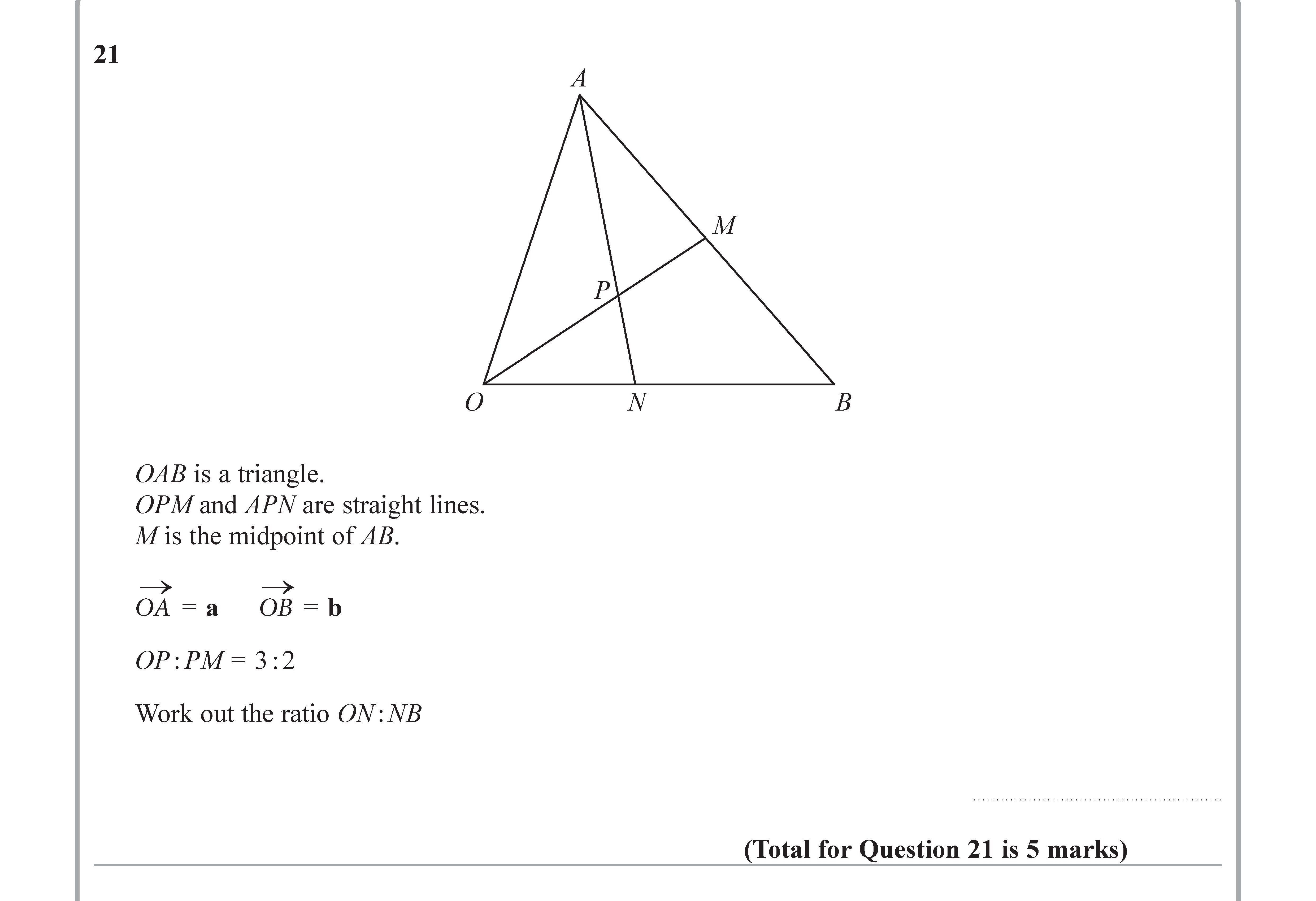
OAB-is-a-triangle-Edexcel-GCSE Maths-Question 22-2018-Paper 1.png

OAB is a triangle. OPM and APN are straight lines. M is the midpoint of AB. $$ \vec{OA} = a \ \vec{OB} = b $$ Work out the ratio ON : NB.

Worked Solution & Example Answer:OAB is a triangle - Edexcel - GCSE Maths - Question 22 - 2018 - Paper 1

Step 1

Process to find \( \vec{OM} \)

96%

114 rated

Answer

Since M is the midpoint of AB, we can express ( \vec{OM} ) as:

OM⃗=12(OA⃗+OB⃗)=12(a+b)\vec{OM} = \frac{1}{2}(\vec{OA} + \vec{OB}) = \frac{1}{2}(a + b)

Step 2

Process to find \( \vec{AP} \)

99%

104 rated

Answer

Using the coordinates of point P on line ON, we can write:

OP⃗=x⋅OA⃗+y⋅OB⃗\vec{OP} = x \cdot \vec{OA} + y \cdot \vec{OB}

where ( x + y = 1 ) and for ( OP:PM = 3:2 ), we find that ( x = 0.6 ) and ( y = 0.4 ). Therefore, we can conclude that:

OP⃗=0.6a+0.4b\vec{OP} = 0.6a + 0.4b

Step 3

Process to find \( \vec{ON} \)

96%

101 rated

Answer

Let ( \vec{ON} = k \cdot \vec{OP} ). Thus,

ON⃗=k(0.6a+0.4b)\vec{ON} = k(0.6a + 0.4b)

From the ratio we set up using segments, we can say that: ( ON:NB = 3:2 ). Therefore, using the comparison based on the sections derived, we reach:

ONNB=32\frac{ON}{NB} = \frac{3}{2}

Join the GCSE students using SimpleStudy...

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;