Photo AI
The diagram shows three circles, each of radius 4 cm - Edexcel - GCSE Maths - Question 3 - 2022 - Paper 1
Question 3
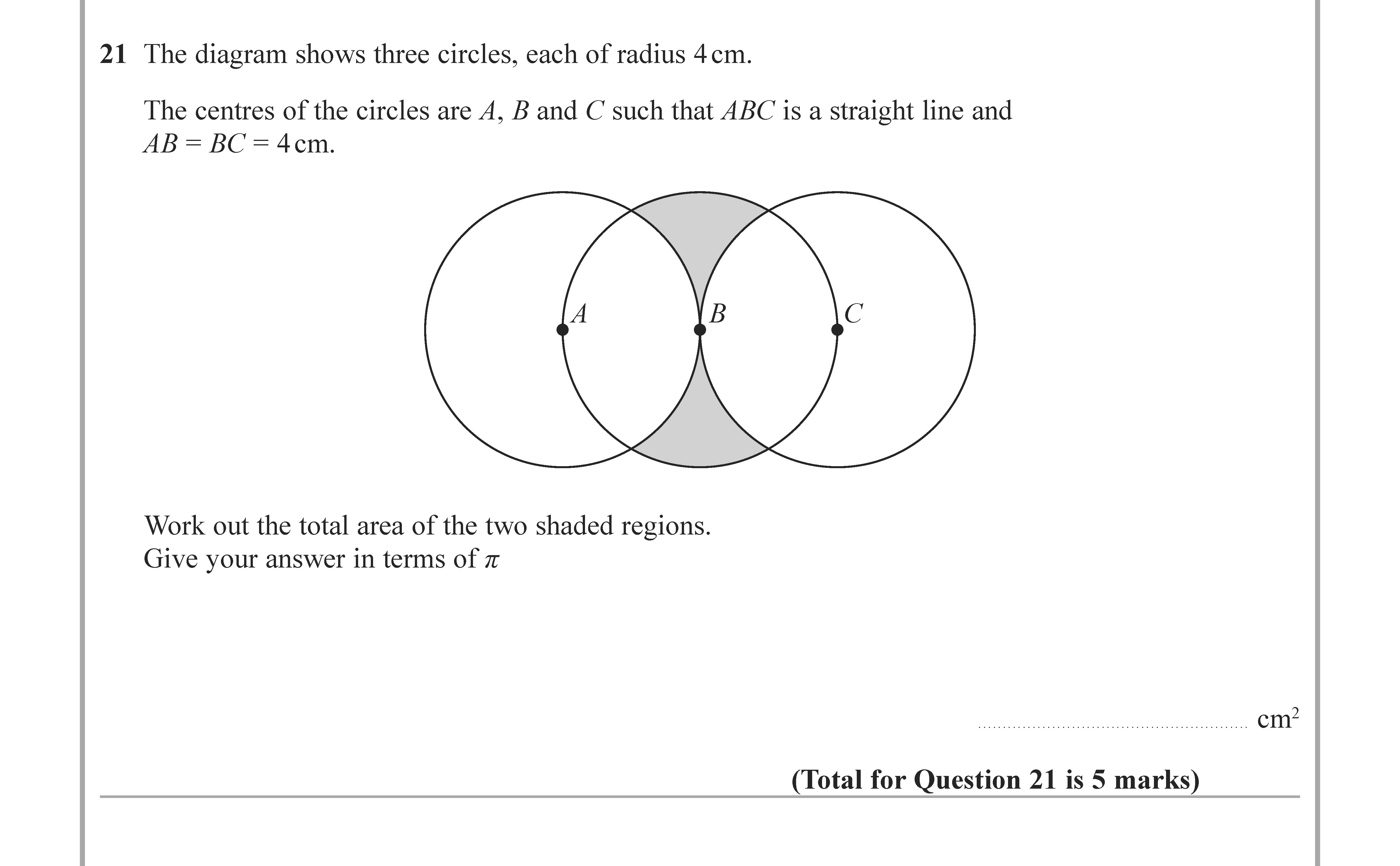
The diagram shows three circles, each of radius 4 cm. The centres of the circles are A, B and C such that ABC is a straight line and AB = BC = 4 cm. Work out the t... show full transcript
Worked Solution & Example Answer:The diagram shows three circles, each of radius 4 cm - Edexcel - GCSE Maths - Question 3 - 2022 - Paper 1
Step 1
Step 2
Calculate the area of the isosceles triangle formed.
Answer
The area of the isosceles triangle can be found using the formula:
Where b is the base (which is the distance between points B and C, 4 cm), and h is the height from A to the base BC. Since the height forms another triangle where the height is equivalent to the distance from the center of the circle to the midpoint of AC.
Using the Pythagorean theorem, the height can be computed as:
Thus, the area is:
Step 3
Step 4
