Photo AI
The diagram shows triangle ABC - Edexcel - GCSE Maths - Question 19 - 2019 - Paper 3
Question 19
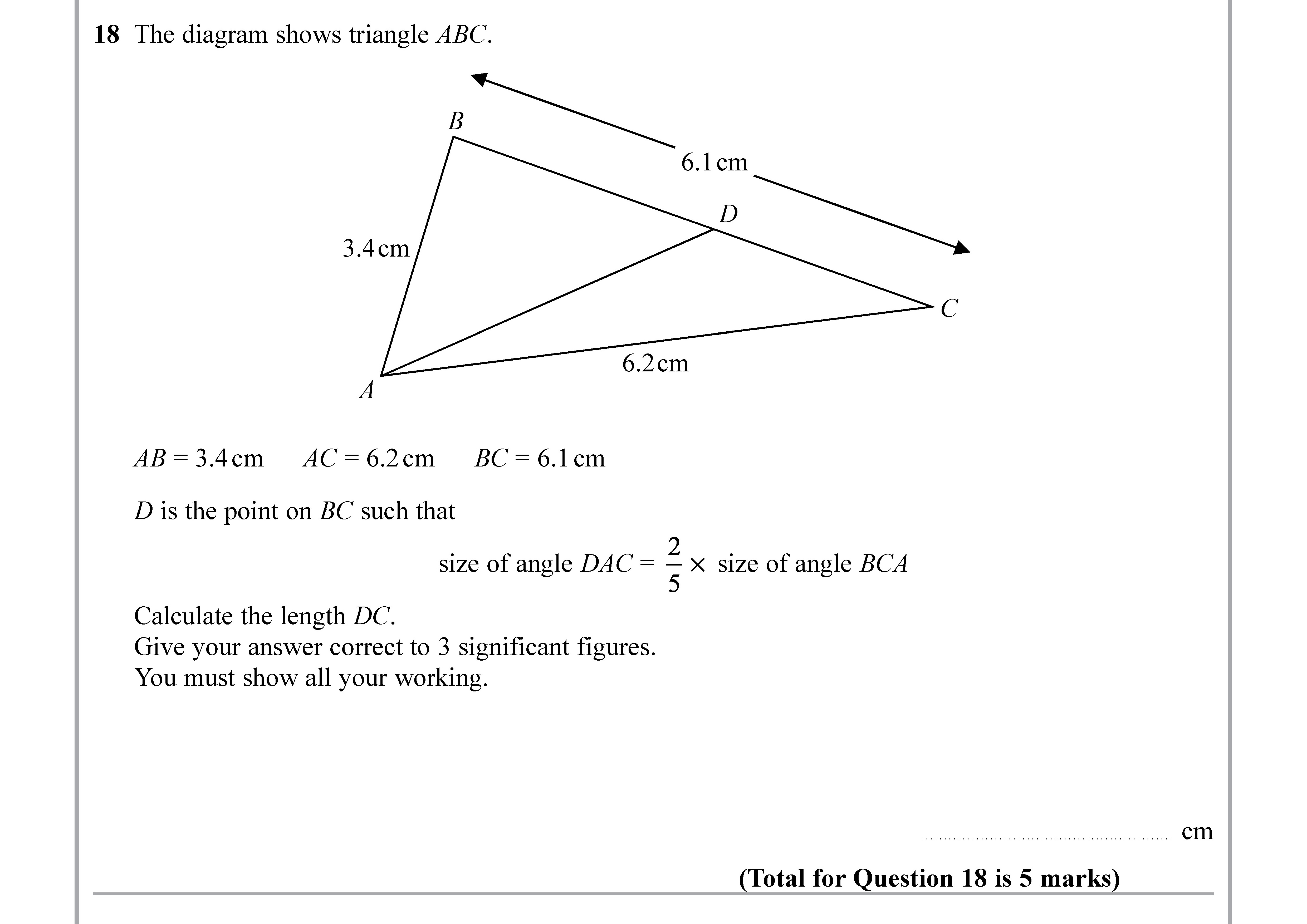
The diagram shows triangle ABC. AB = 3.4 cm AC = 6.2 cm BC = 6.1 cm D is the point on BC such that size of angle DAC = \frac{2}{5} \text{ size of angle BCA} Calcu... show full transcript
Worked Solution & Example Answer:The diagram shows triangle ABC - Edexcel - GCSE Maths - Question 19 - 2019 - Paper 3
Step 1
size of angle DAC = \frac{2}{5} size of angle BCA
Answer
Let ( x ) be the size of angle BCA. Then: [ \text{size of angle DAC} = \frac{2}{5} x ]
According to the triangle properties, we can relate the angles to the sides using the sine rule: [ \frac{AB}{\sin(\text{angle DAC})} = \frac{AC}{\sin(\text{angle BCA})} ]
Substituting the known values: [ \frac{3.4}{\sin(\frac{2}{5} x)} = \frac{6.2}{\sin(x)} ]
Cross multiplying gives: [ 3.4 \sin(x) = 6.2 \sin(\frac{2}{5} x) ]
This relationship will help find ( DC ).
Step 2
Calculate the length DC
Answer
First, we find ( \sin(\frac{2}{5}x) ) using the double angle formula: [ \sin(\frac{2}{5} x) = 2 \sin(\frac{x}{2}) \cos(\frac{x}{2}) ]
Next, we solve the above relation for ( x ) and substitute back into the sine rule.
Using calculated angles, we find the remaining side lengths. Once we determine the corresponding angle for triangle ADC, we can apply the cosine rule: [ DC = \sqrt{AC^2 + AD^2 - 2 \cdot AC \cdot AD \cdot \cos(\text{angle ADC})} ]
After completing the calculation, obtain the value of ( DC ) to three significant figures.
