Photo AI
A car moves from rest - Edexcel - GCSE Maths - Question 15 - 2019 - Paper 2
Question 15
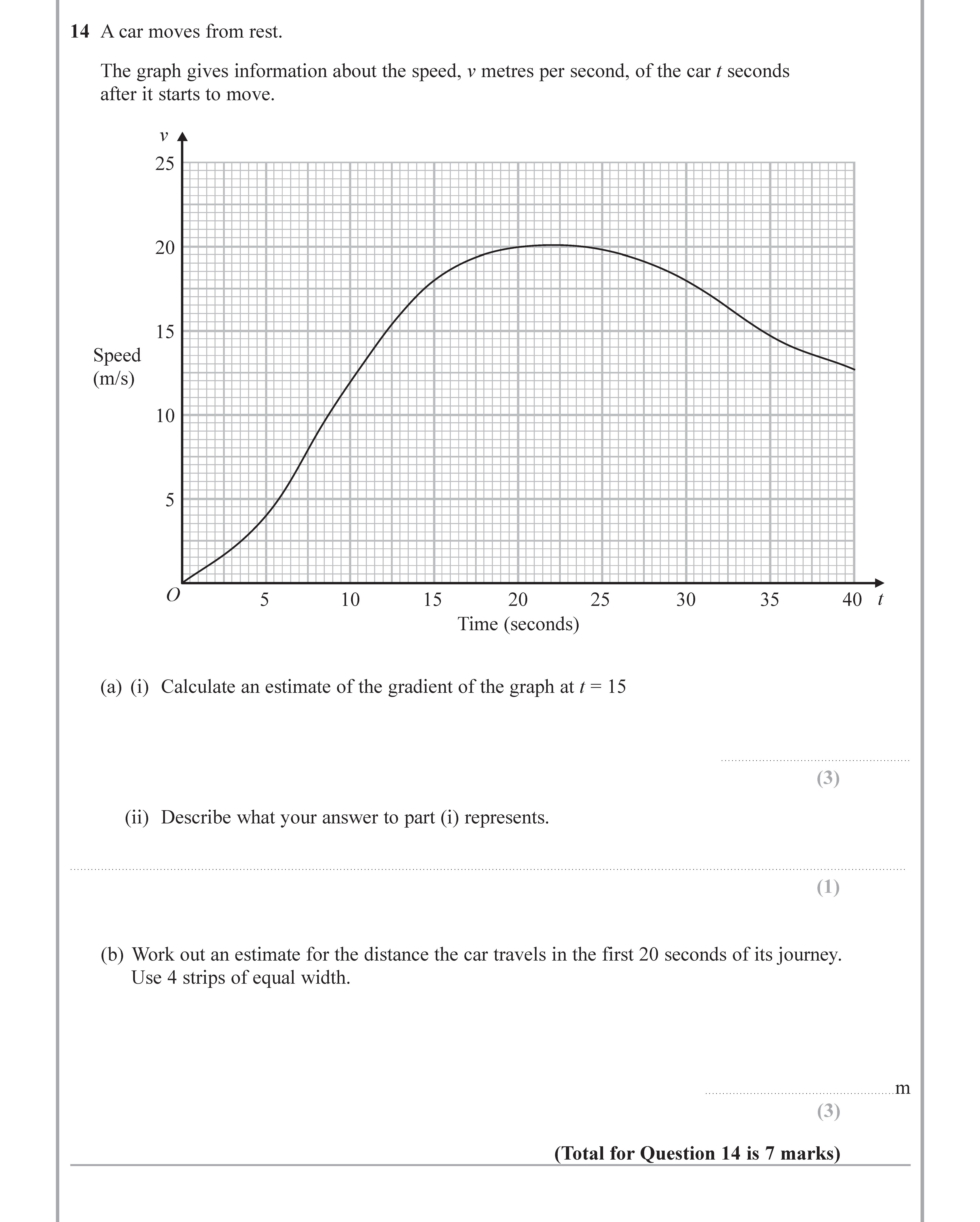
A car moves from rest. The graph gives information about the speed, v metres per second, of the car / seconds after it starts to move. (a) (i) Calculate an estima... show full transcript
Worked Solution & Example Answer:A car moves from rest - Edexcel - GCSE Maths - Question 15 - 2019 - Paper 2
Step 1
Calculate an estimate of the gradient of the graph at t = 15.
Answer
To find the gradient of the graph at t = 15 seconds, we will need to calculate the slope using a tangent line drawn at this point. We can estimate the change in speed over a small interval around t = 15 seconds.
From the graph:
- At t = 10 seconds, the speed is approximately 20 m/s.
- At t = 20 seconds, the speed is approximately 20 m/s.
Since the speed remains constant between t = 10 and t = 20 seconds, the estimated gradient or slope at t = 15 seconds can be calculated as:
Gradient = ( \frac{\Delta v}{\Delta t} = \frac{20 - 20}{20 - 10} = \frac{0}{10} = 0 \text{ m/s}^2 ).
Thus, the gradient at t = 15 seconds is approximately 0.
Step 2
Describe what your answer to part (i) represents.
Answer
The gradient of the graph at t = 15 seconds represents the acceleration of the car at that point in time. Since the gradient is 0, it indicates that the car is moving at a constant speed at that moment, meaning there is no acceleration.
Step 3
Work out an estimate for the distance the car travels in the first 20 seconds of its journey. Use 4 strips of equal width.
Answer
To estimate the distance traveled in the first 20 seconds, we can use the trapezoidal rule or approximate the area under the speed-time graph by dividing it into segments.
We will split the first 20 seconds into 4 equal strips, each of width 5 seconds.
The speed at the following times (estimate from the graph):
- At t = 0 seconds: 0 m/s
- At t = 5 seconds: approximately 10 m/s
- At t = 10 seconds: approximately 20 m/s
- At t = 15 seconds: approximately 20 m/s
- At t = 20 seconds: approximately 15 m/s
Now we can calculate the areas of the trapezoids formed:
- Area from 0 to 5 seconds: ( \frac{1}{2} \times (0 + 10) \times 5 = 25 ) m
- Area from 5 to 10 seconds: ( \frac{1}{2} \times (10 + 20) \times 5 = 75 ) m
- Area from 10 to 15 seconds: ( \frac{1}{2} \times (20 + 20) \times 5 = 100 ) m
- Area from 15 to 20 seconds: ( \frac{1}{2} \times (20 + 15) \times 5 = 87.5 ) m
Adding these areas together:
Total distance = 25 + 75 + 100 + 87.5 = 287.5 m.
Therefore, the estimated distance the car travels in the first 20 seconds is approximately 287.5 m.
