ABCDEF GHI is a cuboid - Edexcel - GCSE Maths - Question 20 - 2022 - Paper 2

Question 20
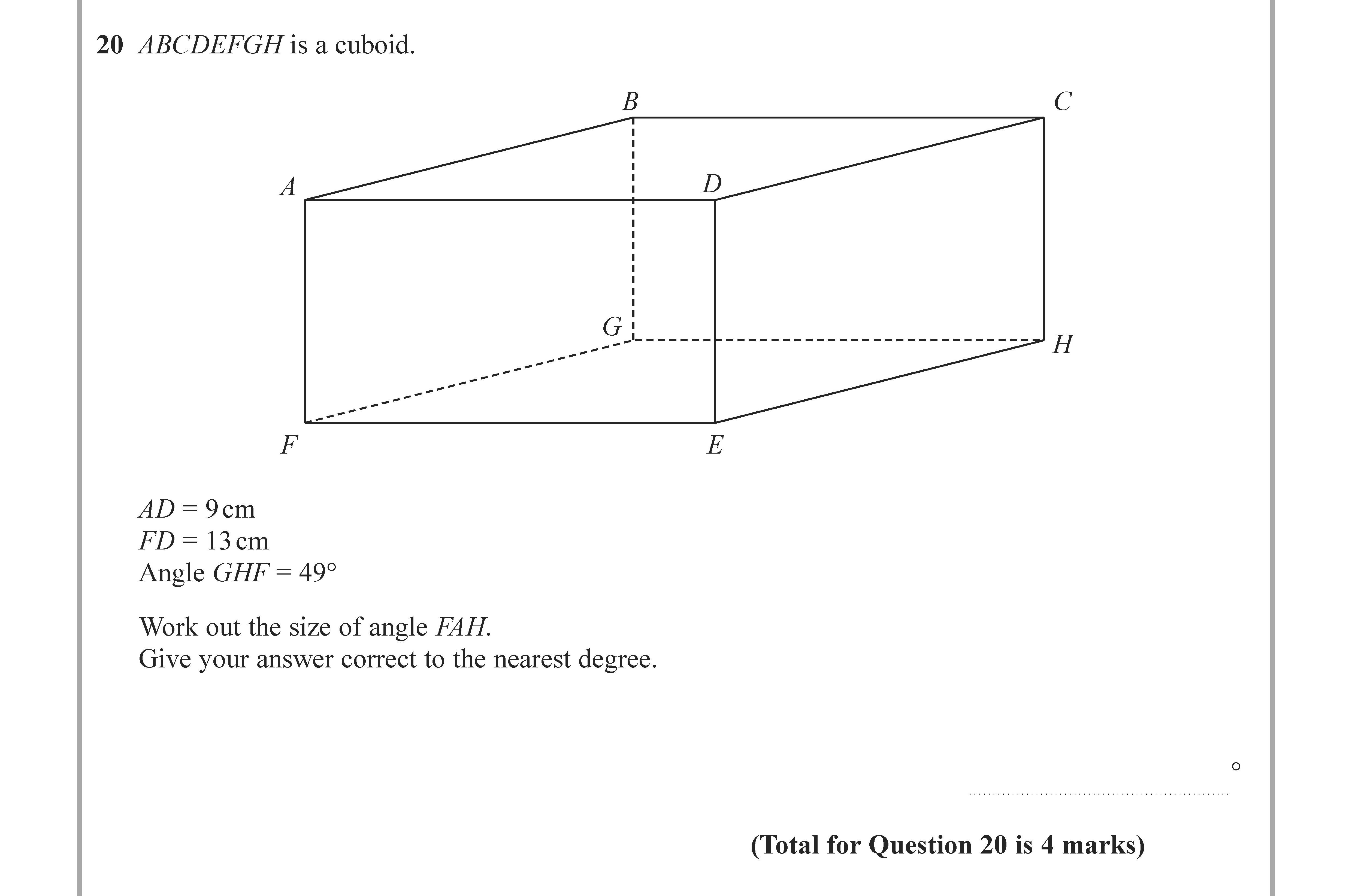
ABCDEF GHI is a cuboid.
AD = 9 cm
FD = 13 cm
Angle GHF = 49°.
Work out the size of angle FAH.
Give your answer correct to the nearest degree.
Worked Solution & Example Answer:ABCDEF GHI is a cuboid - Edexcel - GCSE Maths - Question 20 - 2022 - Paper 2
Work out the size of angle FAH

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To find angle FAH, we can use the cosine rule in triangle AFD. We know the lengths of two sides and the included angle.
-
Identify the given lengths:
- AD = 9 cm
- FD = 13 cm
- Angle GHF = 49° implies angle AFG = 90° - 49° = 41°.
-
Using the sine rule:
- In triangle AFG, applying the sine rule:
sin(GHF)AF=sin(FAH)AD
We need to find AF first. To find AF, we can use the cosine rule in triangle AFD:
AF2=AD2+FD2−2⋅AD⋅FD⋅cos(41°)
AF2=92+132−2⋅9⋅13⋅cos(41°)
Calculate AF:
AF2=81+169−234⋅cos(41°)≈250−234⋅0.7547≈250−176.83
So,
AF2≈73.17⇒AF≈8.55cm
-
Calculating angle FAH:
Now plug this in the sine rule:
sin(49°)AF=sin(FAH)9
Rearranging gives:
sin(FAH)=AF9⋅sin(49°)
Substitute the value of AF:
sin(FAH)=8.559⋅sin(49°)
Compute:
- Assume ( \sin(49°) \approx 0.7547 )
( \sin(FAH) \approx \frac{9 \cdot 0.7547}{8.55} \approx 0.7933 )
-
Final step:
To find angle FAH:
( FAH = \arcsin(0.7933) \approx 52.4° )
Rounding gives angle FAH = 52°.
Join the GCSE students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered

