Photo AI
Here is a pyramid with a square base ABCD - Edexcel - GCSE Maths - Question 13 - 2018 - Paper 3
Question 13
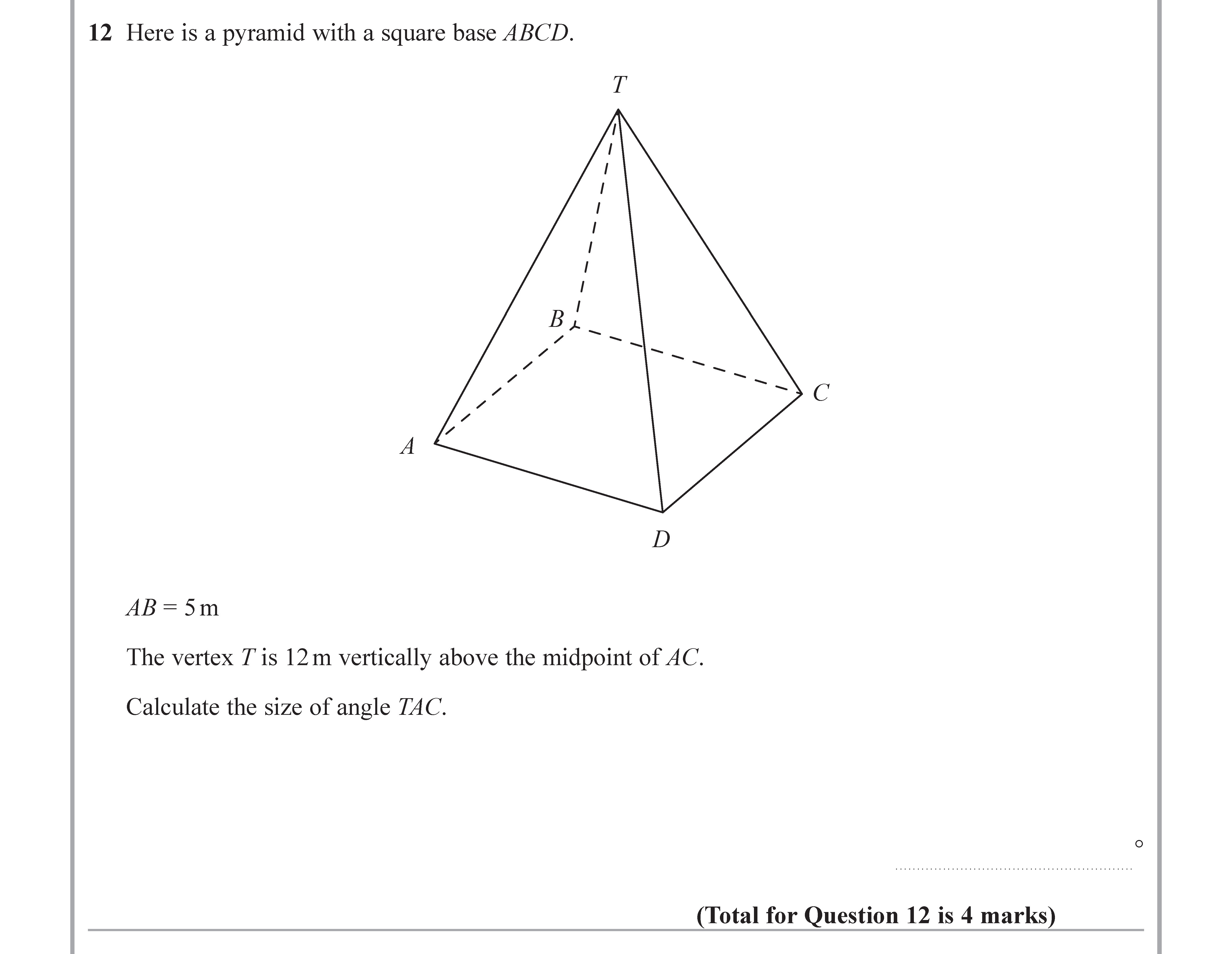
Here is a pyramid with a square base ABCD. AB = 5 m The vertex T is 12 m vertically above the midpoint of AC. Calculate the size of angle TAC.
Worked Solution & Example Answer:Here is a pyramid with a square base ABCD - Edexcel - GCSE Maths - Question 13 - 2018 - Paper 3
Step 1
Step 2
Step 3
Step 4
