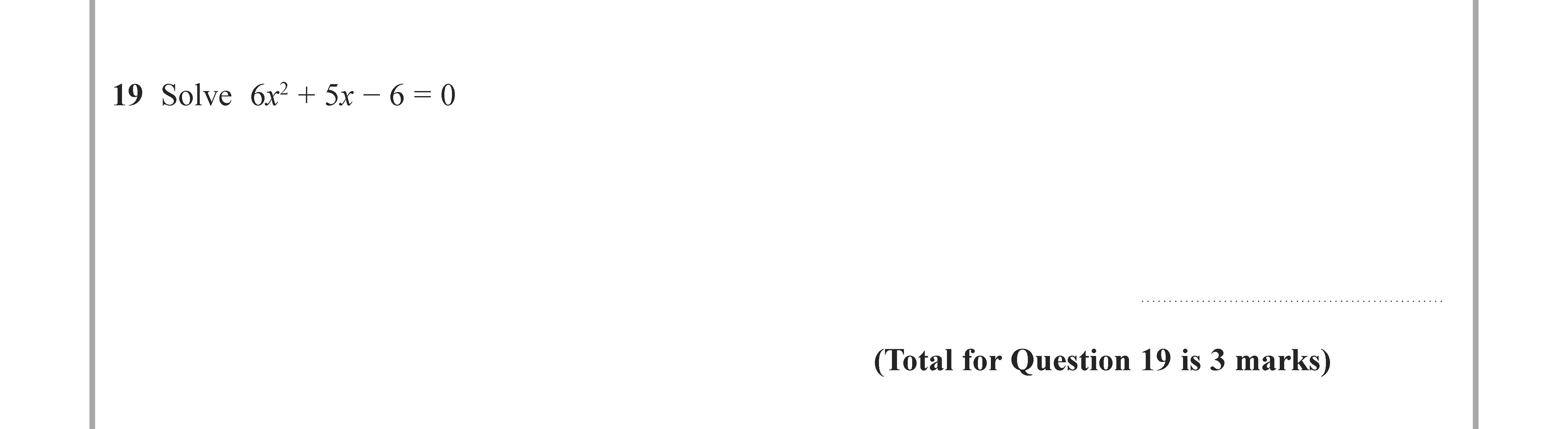Solve $6x^2 + 5x - 6 = 0$ - Edexcel - GCSE Maths - Question 19 - 2022 - Paper 2

Question 19
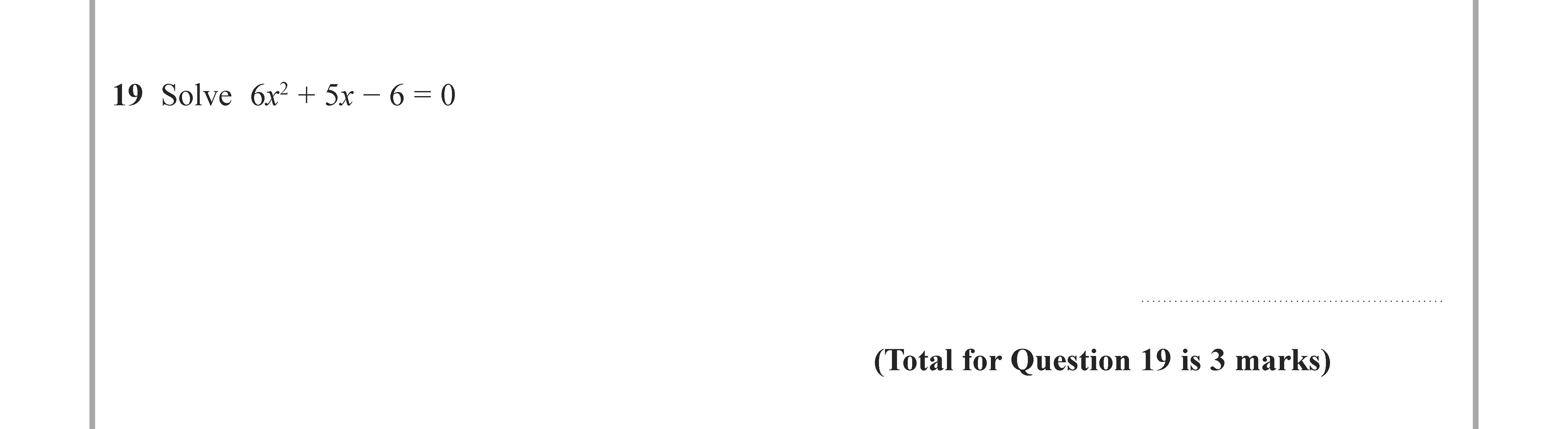
Solve $6x^2 + 5x - 6 = 0$
Worked Solution & Example Answer:Solve $6x^2 + 5x - 6 = 0$ - Edexcel - GCSE Maths - Question 19 - 2022 - Paper 2
Rearranging the Equation

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
First, we need to ensure that the equation is set to zero, which is already achieved here:
6x2+5x−6=0
Applying the Quadratic Formula

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Since this is a quadratic equation in the form ax2+bx+c=0, we will apply the quadratic formula:
x=2a−b±b2−4ac
Here, a=6, b=5, and c=−6.
Calculating the Solutions

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Now, substituting the values into the formula:
- Calculate the discriminant:
b2−4ac=52−4(6)(−6)=25+144=169
- Now applying the values into the quadratic formula:
x=2(6)−5±169=12−5±13
- This gives two solutions:
- For x=12−5+13=128=32
- For x=12−5−13=12−18=−23
Thus, the solutions are:
x=32,−23
Join the GCSE students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered