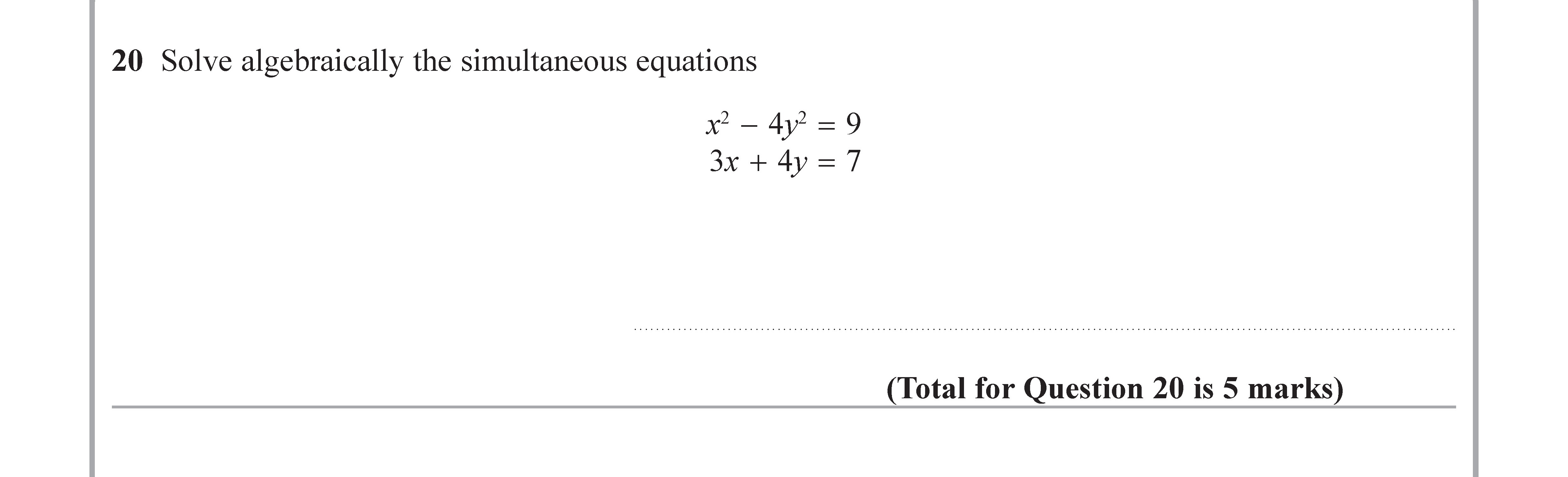Solve algebraically the simultaneous equations
$$
x^2 - 4y = 9
$$
$$
3x + 4y = 7
$$ - Edexcel - GCSE Maths - Question 21 - 2019 - Paper 3

Question 21
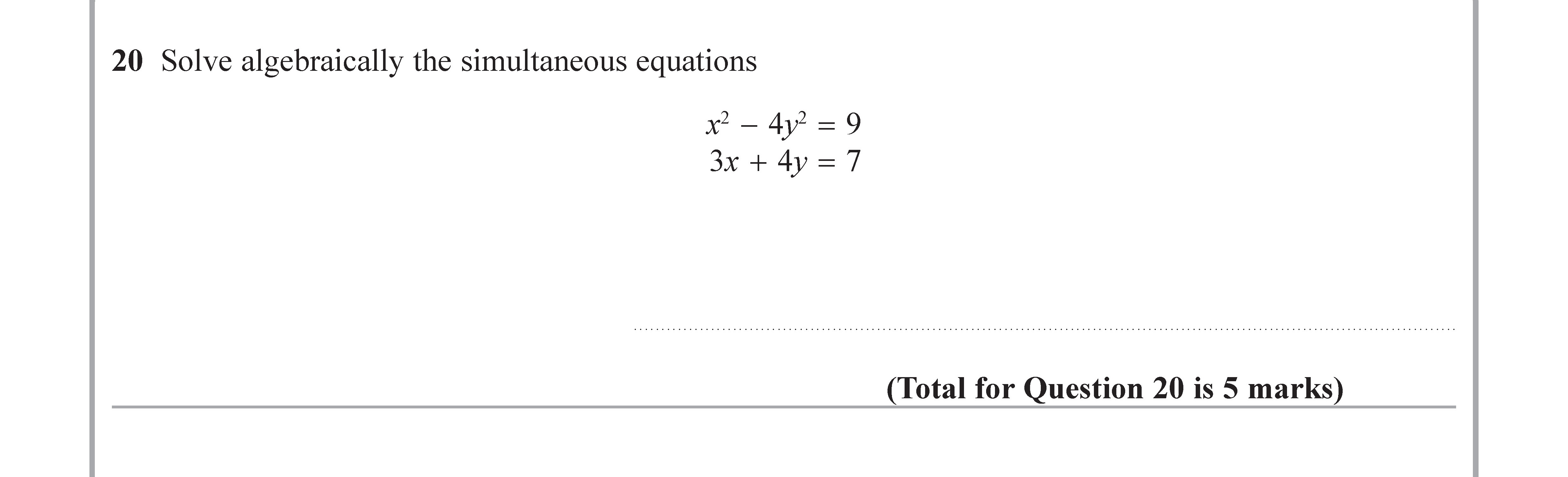
Solve algebraically the simultaneous equations
$$
x^2 - 4y = 9
$$
$$
3x + 4y = 7
$$
Worked Solution & Example Answer:Solve algebraically the simultaneous equations
$$
x^2 - 4y = 9
$$
$$
3x + 4y = 7
$$ - Edexcel - GCSE Maths - Question 21 - 2019 - Paper 3
Substituting for y in the first equation

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Rearranging the first equation, we can isolate y:
4y=x2−9⇒y=4x2−9
Now, substituting this expression for y into the second equation.
Substituting in the second equation

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Substituting into the second equation gives:
3x+4(4x2−9)=7
This simplifies to:
3x+(x2−9)=7
Which further simplifies to:
x2+3x−16=0Factoring the quadratic equation

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
We can factor this quadratic:
(x−4)(x+4)=0
Thus, we find:
x=4extorx=−4Finding corresponding values of y

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Now substituting each value of x back into the expression for y:
-
For x=4:
y=442−9=416−9=47
-
For x=−4:
y=4(−4)2−9=416−9=47
Final solution

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
The two pairs of solutions are:
- For x=4, y=47
- For x=−4, y=47
Thus, the solutions are (4, \frac{7}{4}) and (-4, \frac{7}{4}).
Join the GCSE students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered