GCSE Edexcel Maths Surds: PQR and QRS are triangles. Calc

PQR and QRS are triangles - Edexcel - GCSE Maths - Question 19 - 2022 - Paper 2

Question 19

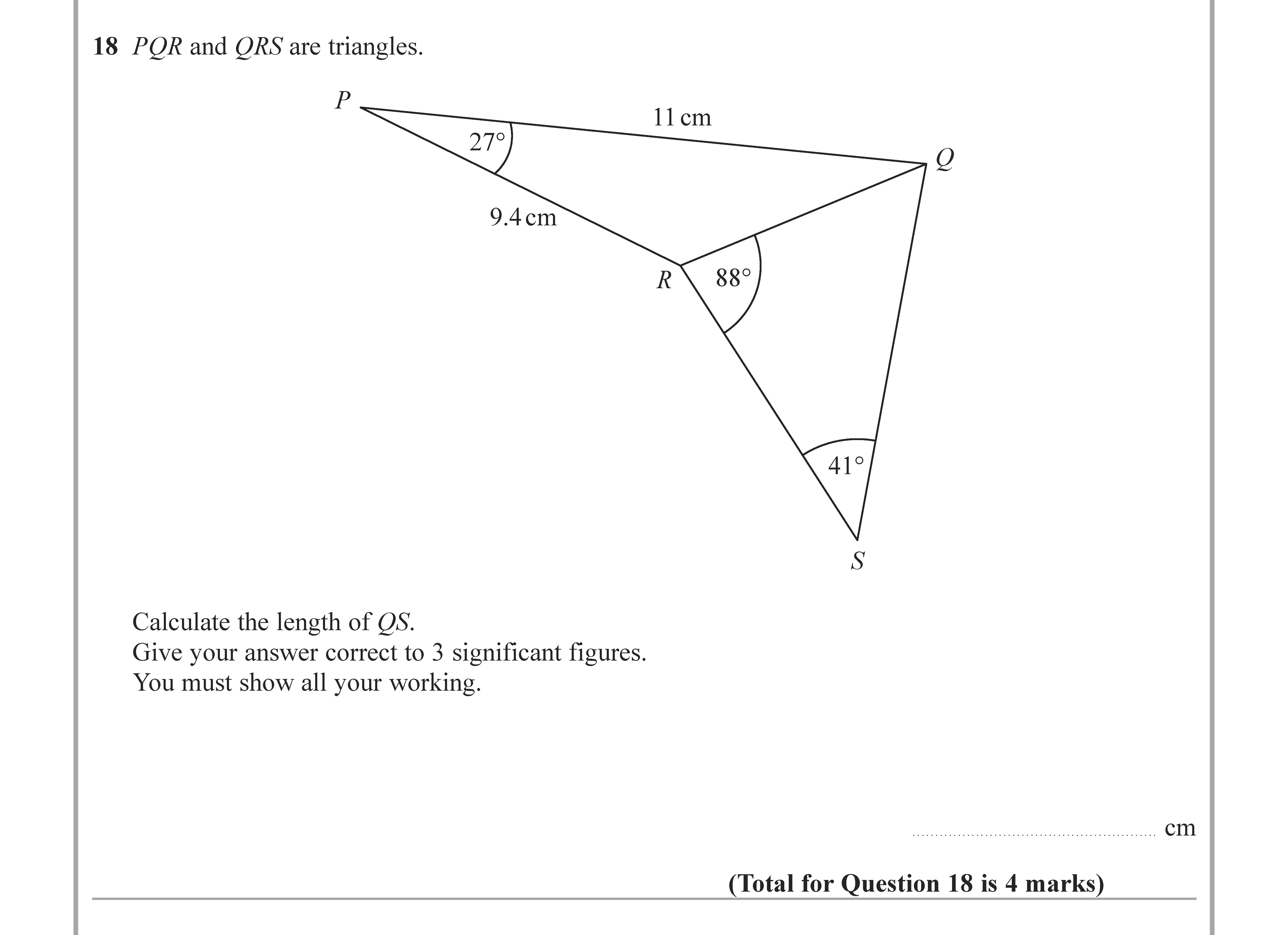
PQR and QRS are triangles. Calculate the length of QS. Give your answer correct to 3 significant figures. You must show all your working. (11 cm, 27°, 9.4 cm, 88°,... show full transcript

Worked Solution & Example Answer:PQR and QRS are triangles - Edexcel - GCSE Maths - Question 19 - 2022 - Paper 2

Step 1

Calculate the length of QR using the sine rule

96%

114 rated

Answer

We can use the sine rule to find the length of QR. According to the sine rule:

$\frac{PQ}{\sin(R)} = \frac{QR}{\sin(P)}$

Substituting the known values:

$\frac{11}{\sin(88^{\circ})} = \frac{QR}{\sin(27^{\circ})}$

Calculating the right side:

Calculate (\sin(88^{\circ}) \approx 0.998)
Calculate (\sin(27^{\circ}) \approx 0.454)

Now rearranging the equation:

$QR = \frac{11 \cdot \sin(27^{\circ})}{\sin(88^{\circ})}$

Substituting:

$QR \approx \frac{11 \cdot 0.454}{0.998} \approx 5.01 \text{ cm}$

Step 2

Calculate the length of QS using the sine rule

99%

104 rated

Answer

Now we can use the sine rule again to calculate QS:

$\frac{QR}{\sin(S)} = \frac{QS}{\sin(Q)}$

Where (S=41^{\circ}) and (Q=88^{\circ})

Substituting the known values:

$\frac{5.01}{\sin(41^{\circ})} = \frac{QS}{\sin(88^{\circ})}$

Calculating the right side:

Calculate (\sin(41^{\circ}) \approx 0.656)

Rearranging gives:

$QS = \frac{5.01 \cdot \sin(88^{\circ})}{\sin(41^{\circ})}$

Substituting:

$QS \approx \frac{5.01 \cdot 0.998}{0.656} \approx 7.63 \text{ cm}$

Rounding to 3 significant figures, the answer is 7.63 cm.

PQR and QRS are triangles - Edexcel - GCSE Maths - Question 19 - 2022 - Paper 2

Worked Solution & Example Answer:PQR and QRS are triangles - Edexcel - GCSE Maths - Question 19 - 2022 - Paper 2

Calculate the length of QR using the sine rule

Calculate the length of QS using the sine rule

Join the GCSE students using SimpleStudy...