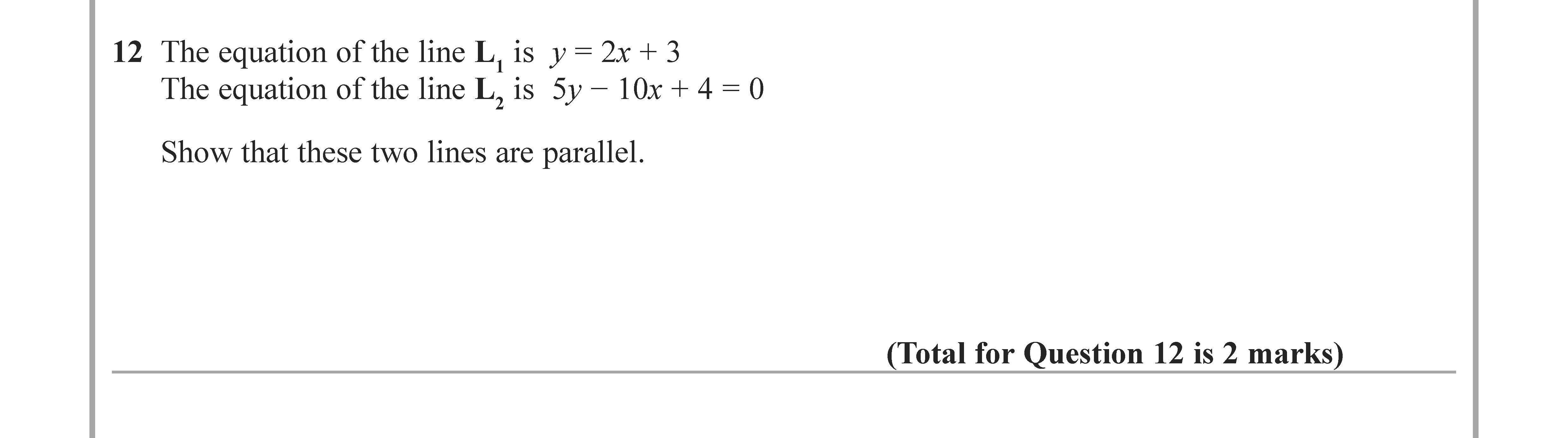The equation of the line L1 is $y = 2x + 3$ - Edexcel - GCSE Maths - Question 13 - 2022 - Paper 2

Question 13
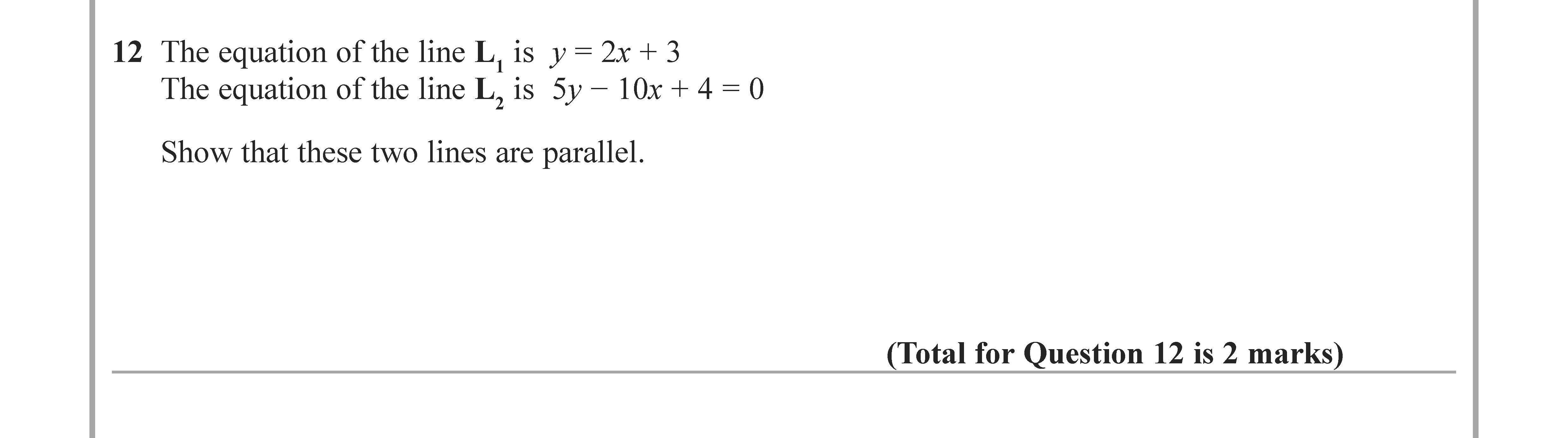
The equation of the line L1 is $y = 2x + 3$.
The equation of the line L2 is $5y - 10x + 4 = 0$.
Show that these two lines are parallel.
Worked Solution & Example Answer:The equation of the line L1 is $y = 2x + 3$ - Edexcel - GCSE Maths - Question 13 - 2022 - Paper 2
Rewrite the equation of line L2

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Start by rearranging the equation of line L2 to the slope-intercept form (y = mx + b).
Given:
5y−10x+4=0
Add 10x to both sides:
5y=10x−4
Now, divide every term by 5:
y = 2x - �rac{4}{5}
Identify the slopes of the lines

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
From the equation of line L1, which is y=2x+3, we can see that the slope (m) is 2.
From the rearranged equation of line L2, y = 2x - �rac{4}{5}, the slope is also 2.
Thus, both lines have the same slope, which is an essential characteristic of parallel lines.
Conclusion

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Since both line L1 and line L2 have the same slope of 2, we can conclude that these two lines are parallel.
Join the GCSE students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered