The diagram shows two shaded shapes, A and B. Shape A is formed by removing a sector of a circle with radius $(3x - 1)$ cm from a sector of the circle with radius $(5 - 1)$ cm. Shape B is a circle of diameter $(2 - 2x)$ cm. The area of shape A is equal to the area of shape B. Find the value of $x$. You must show all your working.

GCSE Edexcel Maths Volume, Area & Surface Area: The diagram shows two shaded sha

The diagram shows two shaded shapes, A and B - Edexcel - GCSE Maths - Question 22 - 2020 - Paper 1

Question 22

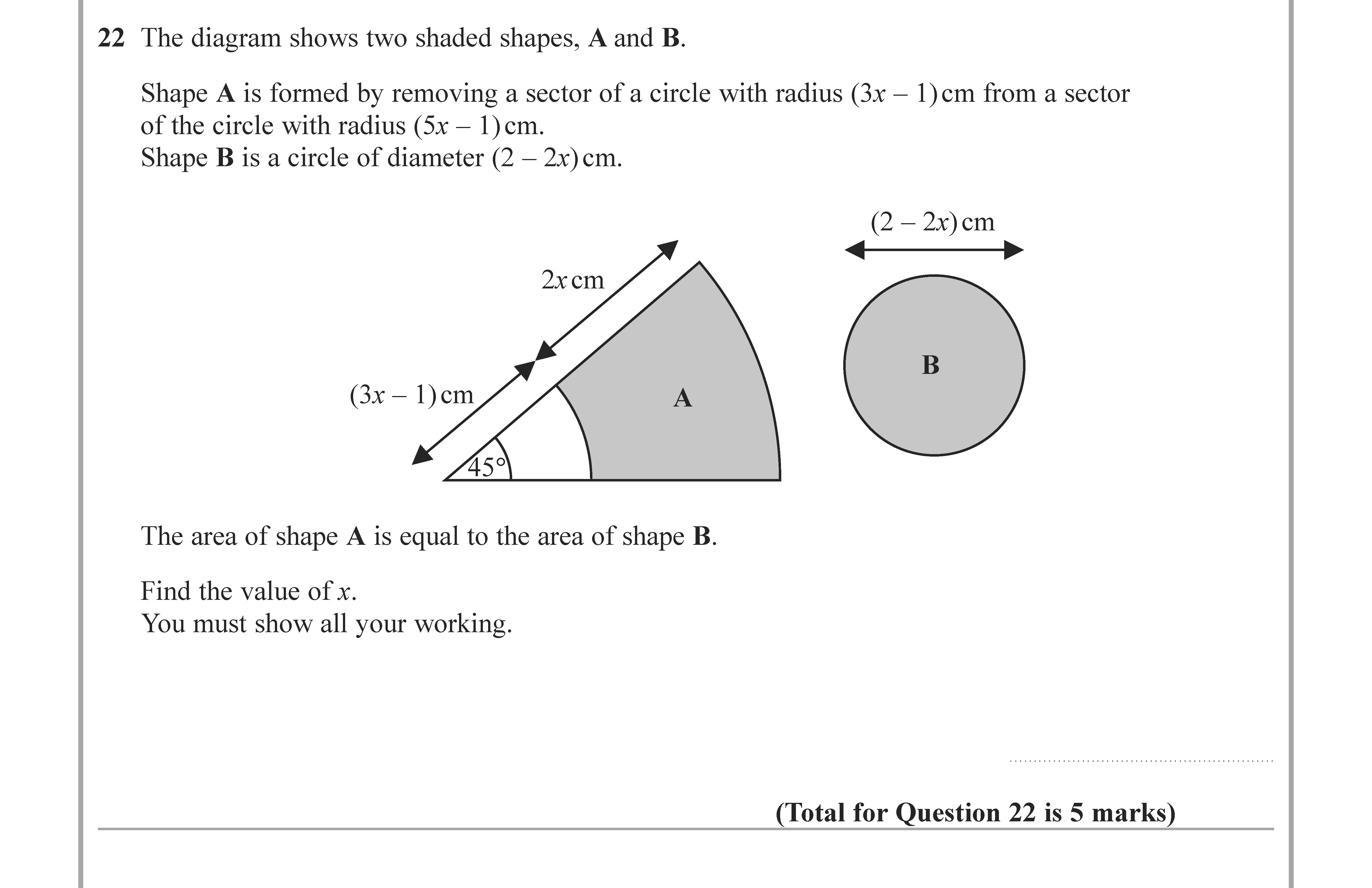
The diagram shows two shaded shapes, A and B. Shape A is formed by removing a sector of a circle with radius $(3x - 1)$ cm from a sector of the circle with radius $... show full transcript

Worked Solution & Example Answer:The diagram shows two shaded shapes, A and B - Edexcel - GCSE Maths - Question 22 - 2020 - Paper 1

Step 1

Derive an algebraic expression for the area of A

96%

114 rated

Answer

To find the area of shape A, we first need to calculate the area of the sector of the larger circle and subtract the area of the smaller sector:

For the larger circle with radius $4$ cm (since $5 - 1 = 4$ ):

The area of a sector is given by: $\text{Area} = \frac{1}{2} r^2 \theta$

For shape A, we can write: $\text{Area}_A = \frac{1}{2} (5 - 1)^2 \theta - \frac{1}{2} (3x - 1)^2 \theta$

Factoring out $heta$ , we obtain: $\text{Area}_A = \frac{\theta}{2} \left( 16 - (9x^2 - 6x + 1) \right) = \frac{\theta}{2} (15 - 9x^2 + 6x)$

Step 2

Derive an algebraic expression for the area of B

99%

104 rated

Answer

For shape B which is a circle with diameter $(2 - 2x)$ cm, we first find the radius:

The area of circle B is: $\text{Area}_B = \pi r^2 = \pi (1 - x)^2 = \pi (1 - 2x + x^2)$

Step 3

Set the areas equal and rearrange

96%

101 rated

Answer

$\frac{\theta}{2} (15 - 9x^2 + 6x) = \pi (1 - 2x + x^2)$

Assuming $heta \neq 0$ , we simplify this to: $15 - 9x^2 + 6x = \frac{2\pi}{\theta} (1 - 2x + x^2)$

Rearranging to form a quadratic equation gives: $-9x^2 + 6x - \frac{2\pi}{\theta} + \frac{2\pi}{\theta} 2x = 0$

Step 4

Factor or use the quadratic formula to find x

98%

120 rated

Answer

Replacing the values, we simplify: $-9x^2 + (6 + 4\pi)x - \frac{2\pi}{\theta} = 0$

Using the quadratic formula, $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ , we find: $x = \frac{-(6 + 4\pi) \pm \sqrt{(6 + 4\pi)^2 - 4(-9)(-\frac{2\pi}{\theta})}}{2(-9)}$

Thus we can find the value of $x$ .

The diagram shows two shaded shapes, A and B - Edexcel - GCSE Maths - Question 22 - 2020 - Paper 1

Worked Solution & Example Answer:The diagram shows two shaded shapes, A and B - Edexcel - GCSE Maths - Question 22 - 2020 - Paper 1

Derive an algebraic expression for the area of A

Derive an algebraic expression for the area of B

Set the areas equal and rearrange

Factor or use the quadratic formula to find x

Join the GCSE students using SimpleStudy...