Photo AI
The diagram shows a right-angled triangular prism ABCDEF - OCR - GCSE Maths - Question 20 - 2018 - Paper 4
Question 20
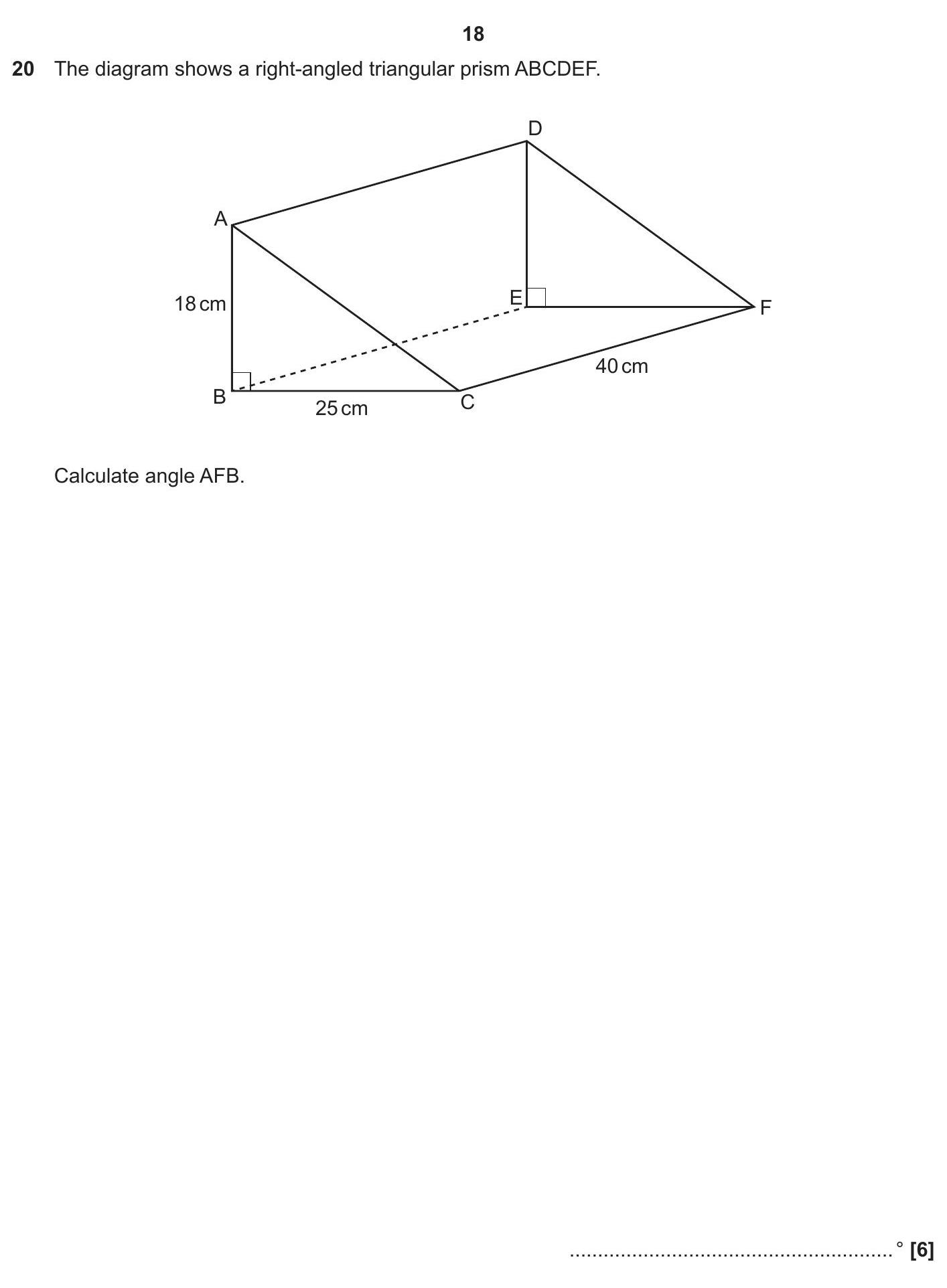
The diagram shows a right-angled triangular prism ABCDEF. Calculate angle AFB.
Worked Solution & Example Answer:The diagram shows a right-angled triangular prism ABCDEF - OCR - GCSE Maths - Question 20 - 2018 - Paper 4
Step 1
Calculate angle AFB using trigonometric functions
Answer
To find angle AFB, we will use the sine function in triangle AFB.
We know:
- AB = 18 cm (height)
- BC = 25 cm (base)
- AF = 40 cm (hypotenuse)
Using the sine function:
Calculating:
To find angle AFB, we will take the inverse sine:
Thus, angle AFB is approximately 26.57 degrees.
Step 2
Verify using cosine rule
Answer
Alternatively, we can verify using the cosine rule:
Using the formula:
Here, AF = 40 cm, AB = 18 cm, and BF = 25 cm.
This gives:
Calculating:
Calculating angle AFB gives approximately the same value when you compute the inverse cosine.
This confirms that angle AFB is consistent, thus concluding our solution.
