Photo AI
10. Simplify - OCR - GCSE Maths - Question 10 - 2020 - Paper 1
Question 10
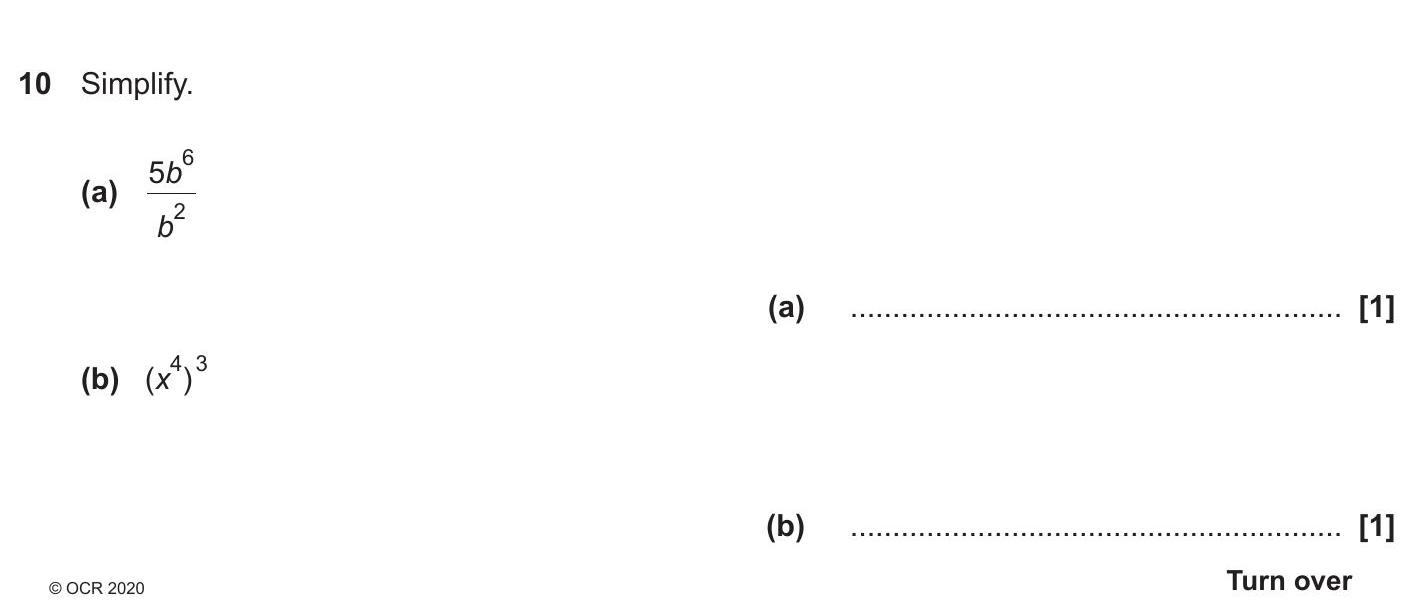
10. Simplify. (a) \( \frac{5b^6}{b^2} \) (b) \( \left( x^{\frac{1}{3}} \right)^{3} \)
Worked Solution & Example Answer:10. Simplify - OCR - GCSE Maths - Question 10 - 2020 - Paper 1
Step 1
(a) \( \frac{5b^6}{b^2} \)
Answer
To simplify ( \frac{5b^6}{b^2} ), we can divide the powers of ( b ):
- Use the quotient rule for exponents: ( \frac{b^m}{b^n} = b^{m-n} ).
- Here, ( m = 6 ) and ( n = 2 ).
- Thus, ( \frac{b^6}{b^2} = b^{6-2} = b^{4} ).
- Therefore, the simplified expression is ( 5b^{4} ).
Step 2
(b) \( \left( x^{\frac{1}{3}} \right)^{3} \)
Answer
To simplify ( \left( x^{\frac{1}{3}} \right)^{3} ), we can apply the power of a power rule for exponents:
- The rule states that ( (a^m)^n = a^{m \cdot n} ).
- Here, we multiply the exponents: ( \frac{1}{3} \cdot 3 = 1 ).
- Therefore, ( \left( x^{\frac{1}{3}} \right)^{3} = x^{1} = x ).
- The simplified expression is simply ( x ).
