6. (a) Simplify fully - OCR - GCSE Maths - Question 6 - 2017 - Paper 1

Question 6
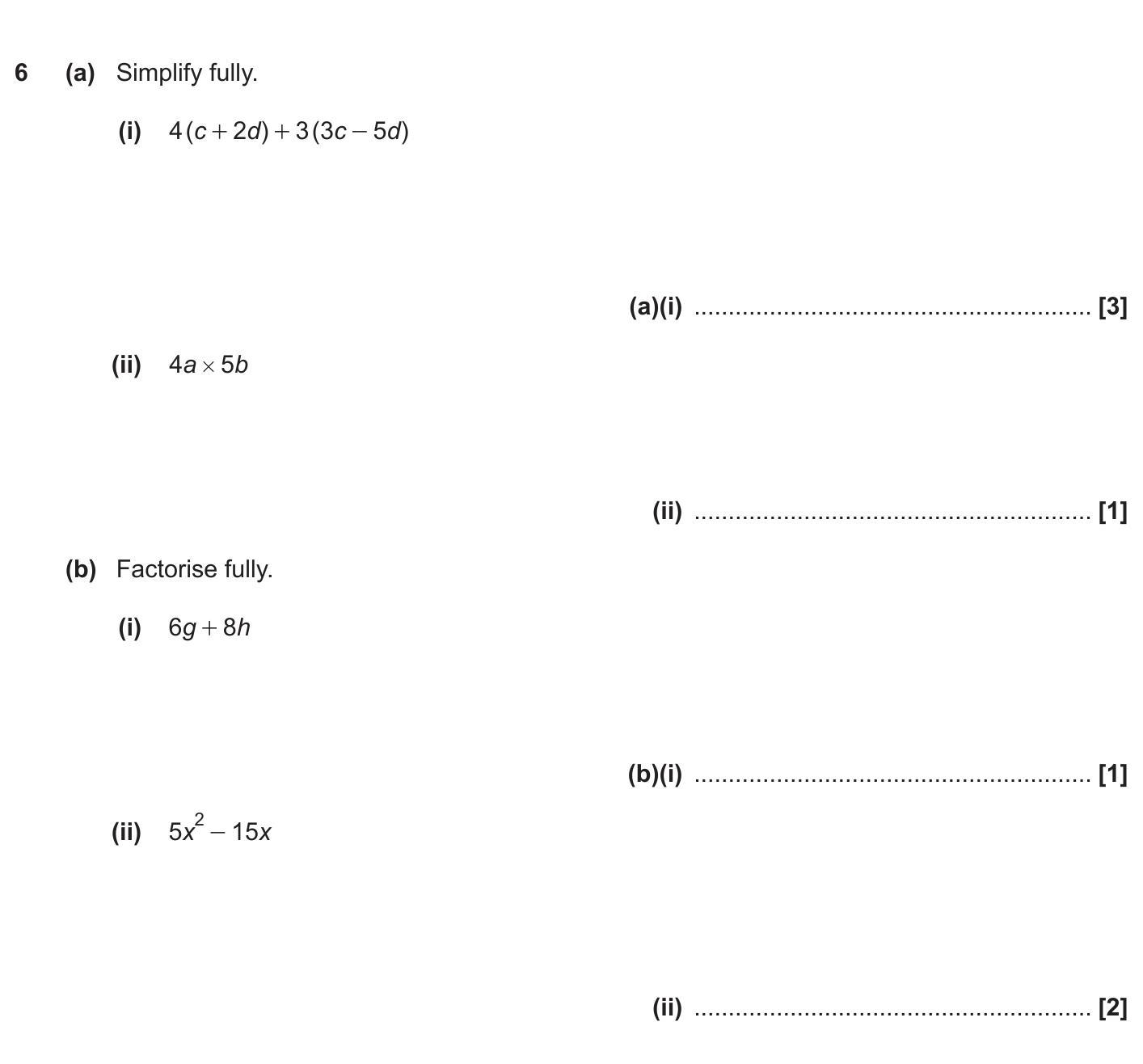
6. (a) Simplify fully.
(i) 4(c + 2d) + 3(3c - 5d)
(ii) 4a × 5b
(b) Factorise fully.
(i) 6g + 8h
(ii) 5x² - 15x
Worked Solution & Example Answer:6. (a) Simplify fully - OCR - GCSE Maths - Question 6 - 2017 - Paper 1
Simplify fully.
(i) 4(c + 2d) + 3(3c - 5d)

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To simplify the expression, we start by distributing the constants into the brackets:
-
Multiply out the terms:
4(c + 2d) &= 4c + 8d, \
3(3c - 5d) &= 9c - 15d.
\\
ext{So the expression becomes:} \
4c + 8d + 9c - 15d.
\\
2. Combine like terms:
\
(4c + 9c) + (8d - 15d) = 13c - 7d.
\\
ext{Thus, the simplified result is:}
\boxed{13c - 7d}.
\end{aligned}$$
Simplify fully.
(ii) 4a × 5b

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To simplify the expression:
-
Multiply the coefficients and the variables separately:
4a×5b=(4×5)(a×b)=20ab.
ext{Thus, the final answer is:}
\boxed{20ab}.
Factorise fully.
(i) 6g + 8h

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To factorise the expression:
-
Identify the greatest common factor (GCF) of the terms:
The GCF of 6g and 8h is 2.
-
Factor out the GCF:
6g+8h=2(3g+4h).
ext{Therefore, the factorised form is:}
\boxed{2(3g + 4h)}.
Factorise fully.
(ii) 5x² - 15x

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To factorise the expression:
-
Identify the greatest common factor (GCF):
The GCF of 5x² and -15x is 5x.
-
Factor out the GCF:
5x2−15x=5x(x−3).
ext{Thus, the factorised form is:}
\boxed{5x(x - 3)}.
Join the GCSE students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered

