Photo AI

1 Work out - OCR - GCSE Maths - Question 1 - 2018 - Paper 5

Question 1

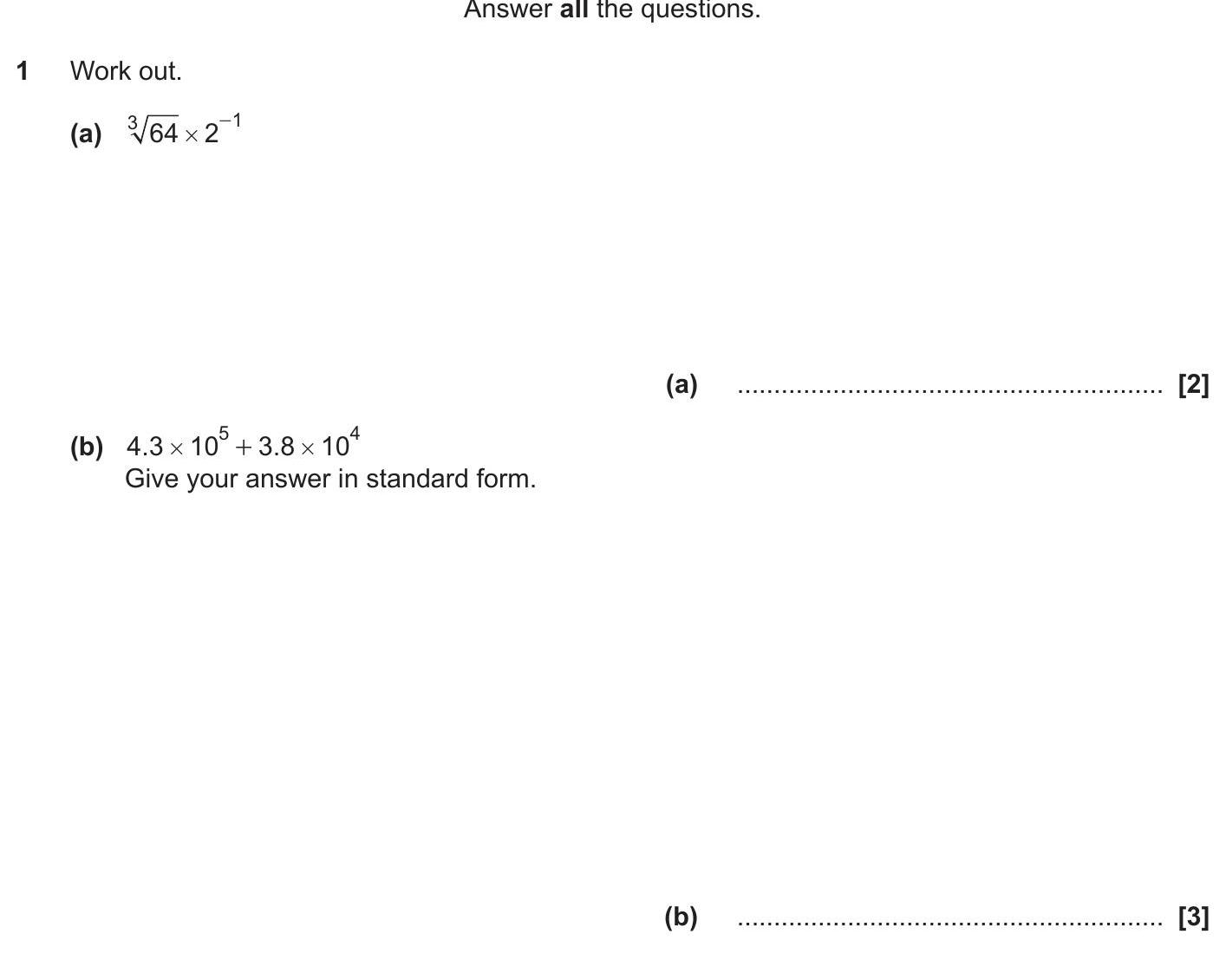
1 Work out. (a) $$\sqrt{64} \times 2^{-1}$$ (b) $$4.3 \times 10^{5} + 3.8 \times 10^{4}$$ Give your answer in standard form.

Worked Solution & Example Answer:1 Work out - OCR - GCSE Maths - Question 1 - 2018 - Paper 5

Step 1

96%

114 rated

Answer

To solve (\sqrt{64} \times 2^{-1}), we first calculate (\sqrt{64} = 8). Next, we evaluate (2^{-1} = \frac{1}{2}). Therefore, the expression becomes:

$8 \times \frac{1}{2} = 4$

Thus, the answer is 4.

Step 2

99%

104 rated

Answer

First, we convert (3.8 \times 10^{4}) to the same power of 10 as (4.3 \times 10^{5}):

$3.8 \times 10^{4} = 0.38 \times 10^{5}$

Now we can add the two terms:

$4.3 \times 10^{5} + 0.38 \times 10^{5} = (4.3 + 0.38) \times 10^{5}$

Calculating the sum gives:

$4.68 \times 10^{5}$

Thus, the answer in standard form is 4.68 × 10⁵.

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;