Photo AI
The diagram shows a circle, centre O - OCR - GCSE Maths - Question 16 - 2020 - Paper 6
Question 16
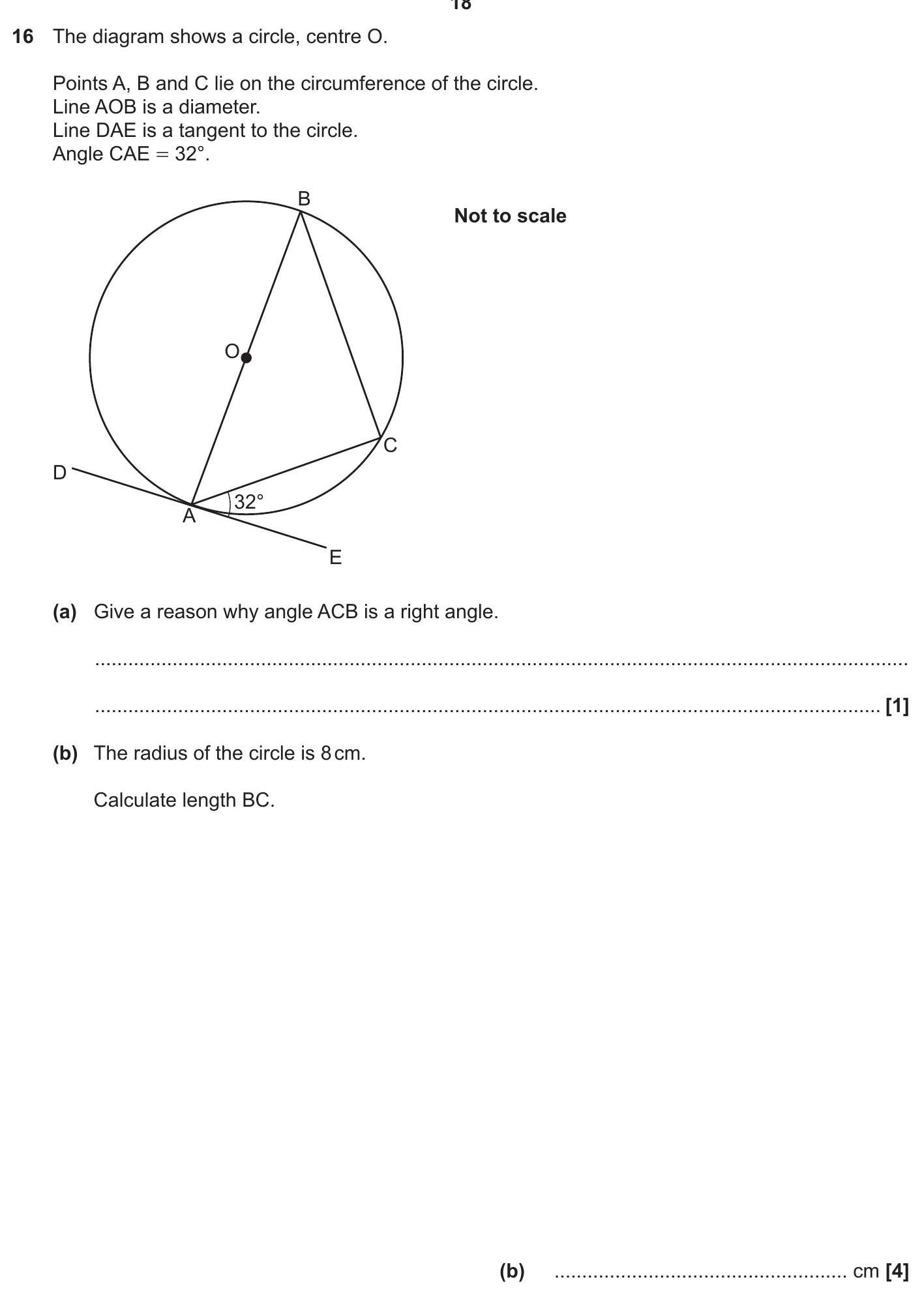
The diagram shows a circle, centre O. Points A, B and C lie on the circumference of the circle. Line AOB is a diameter. Line DAE is a tangent to the circle. Angle C... show full transcript
Worked Solution & Example Answer:The diagram shows a circle, centre O - OCR - GCSE Maths - Question 16 - 2020 - Paper 6
Step 1
Step 2
Calculate length BC.
Answer
Given that the radius of the circle is 8 cm, the diameter AOB is:
To find length BC, we can apply the tangent-secant theorem and the properties of triangles in the circle. The angle CAE is 32°, and angle ACB is 90°.
Using the sine rule in triangle ABC, we have:
Substituting AB:
Calculating this gives:
Thus,
Therefore, rounding this to two decimal places, the length BC is approximately:
