Photo AI

AOB is a sector of a circle, centre O and radius 6 cm - OCR - GCSE Maths - Question 12 - 2018 - Paper 5

Question 12

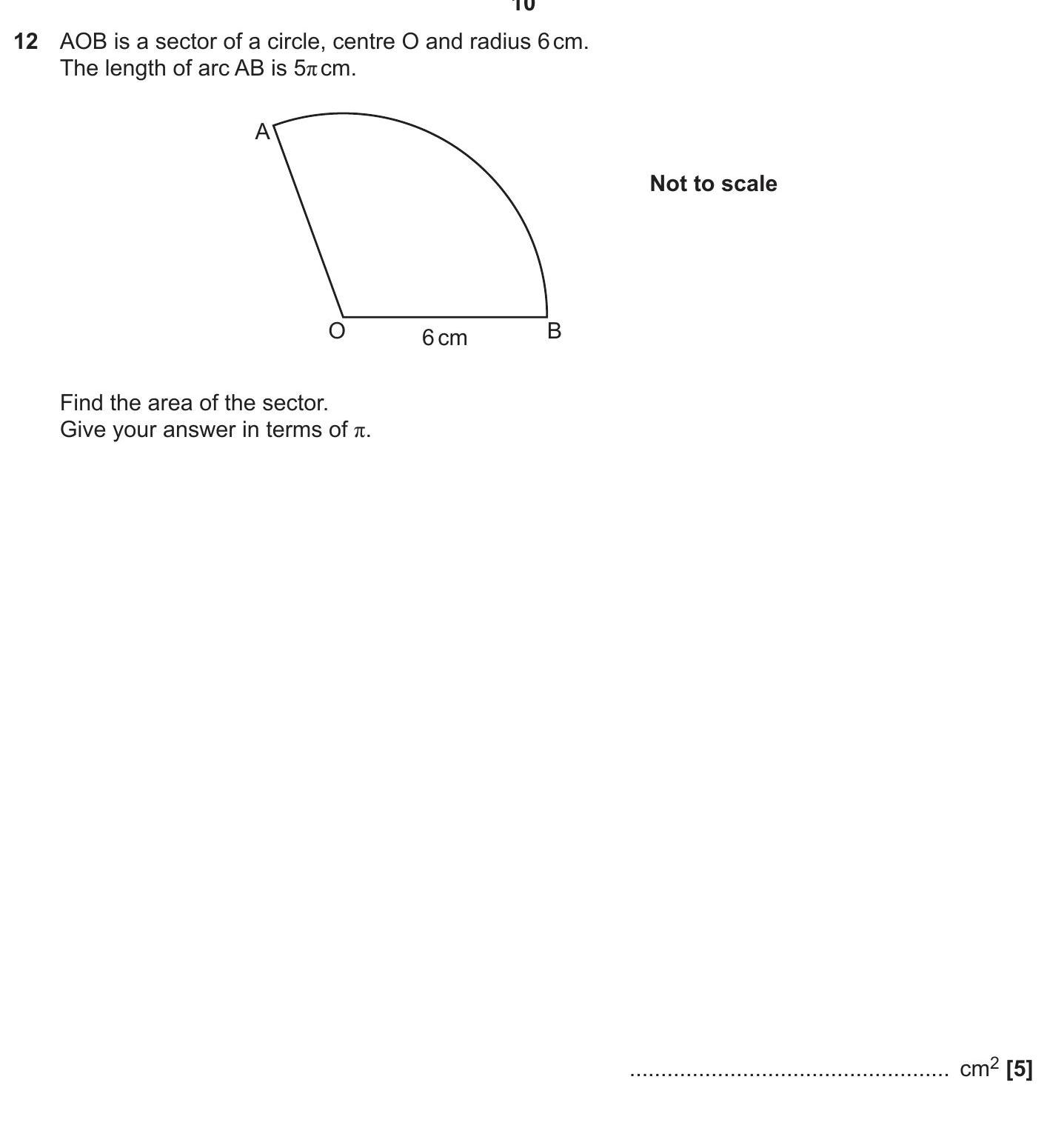
AOB is a sector of a circle, centre O and radius 6 cm. The length of arc AB is 5 cm. Find the area of the sector. Give your answer in terms of π.

Worked Solution & Example Answer:AOB is a sector of a circle, centre O and radius 6 cm - OCR - GCSE Maths - Question 12 - 2018 - Paper 5

Step 1

96%

114 rated

Answer

To find the angle θ (in radians) at the centre O corresponding to the arc AB, we use the formula for the length of an arc:

$ext{Arc Length} = r imes heta$

Given that the radius r = 6 cm and the arc length = 5 cm, we can rearrange this to find θ:

$heta = \frac{\text{Arc Length}}{r} = \frac{5}{6} \text{ radians}.$

Step 2

99%

104 rated

Answer

The area A of a sector with angle θ (in radians) is given by the formula:

$A = \frac{1}{2} r^2 \theta$

Substituting r = 6 cm and θ = \frac{5}{6}:

$A = \frac{1}{2} \times 6^2 \times \frac{5}{6} = \frac{1}{2} \times 36 \times \frac{5}{6} = \frac{30}{2} = 15.$

Thus, the area of the sector is $15\pi$ square cm.

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;