Photo AI

14. Simplify: (a) $4a^1 \times 3a^2$ (b) $\left( \frac{2a^2}{a^3} \right)^{3}$ - OCR - GCSE Maths - Question 14 - 2020 - Paper 1

Question icon

Question 14

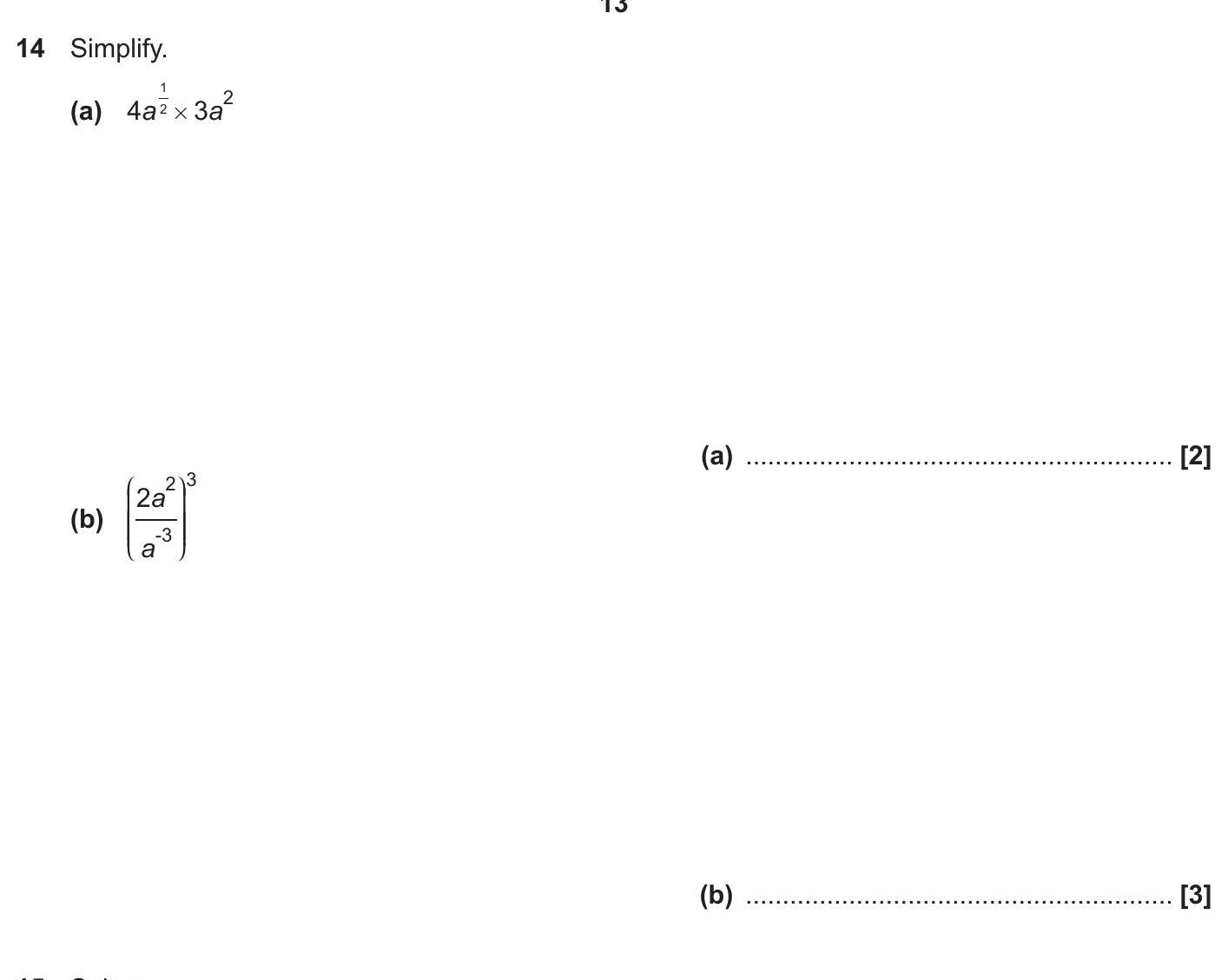
14.-Simplify:--(a)-$4a^1-\times-3a^2$--(b)-$\left(-\frac{2a^2}{a^3}-\right)^{3}$-OCR-GCSE Maths-Question 14-2020-Paper 1.png

14. Simplify: (a) $4a^1 \times 3a^2$ (b) $\left( \frac{2a^2}{a^3} \right)^{3}$

Worked Solution & Example Answer:14. Simplify: (a) $4a^1 \times 3a^2$ (b) $\left( \frac{2a^2}{a^3} \right)^{3}$ - OCR - GCSE Maths - Question 14 - 2020 - Paper 1

Step 1

(a) $4a^1 \times 3a^2$

96%

114 rated

Answer

To simplify the expression, we first multiply the coefficients and then combine the powers of aa.

  1. Multiply the coefficients: 4×3=124 \times 3 = 12.
  2. For the bases with the same exponent, add the exponents: a1×a2=a1+2=a3.a^1 \times a^2 = a^{1+2} = a^3.

Combining these results, we find:

12a312a^3

Step 2

(b) $\left( \frac{2a^2}{a^3} \right)^{3}$

99%

104 rated

Answer

First, simplify the fraction inside the parentheses:

  1. For the aa terms, subtract the exponents: a2a3=a2−3=a−1.\frac{a^2}{a^3} = a^{2-3} = a^{-1}. So, the expression now becomes: 2a.\frac{2}{a}.

  2. Next, raise the simplified expression to the power of 3: (2a)3=23a3=8a3.\left( \frac{2}{a} \right)^{3} = \frac{2^{3}}{a^{3}} = \frac{8}{a^{3}}.

Thus, the final answer is:

8a3\frac{8}{a^3}

Join the GCSE students using SimpleStudy...

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;