Photo AI
The probability that Sam works from home on Monday is 0.4 - OCR - GCSE Maths - Question 24 - 2023 - Paper 1
Question 24
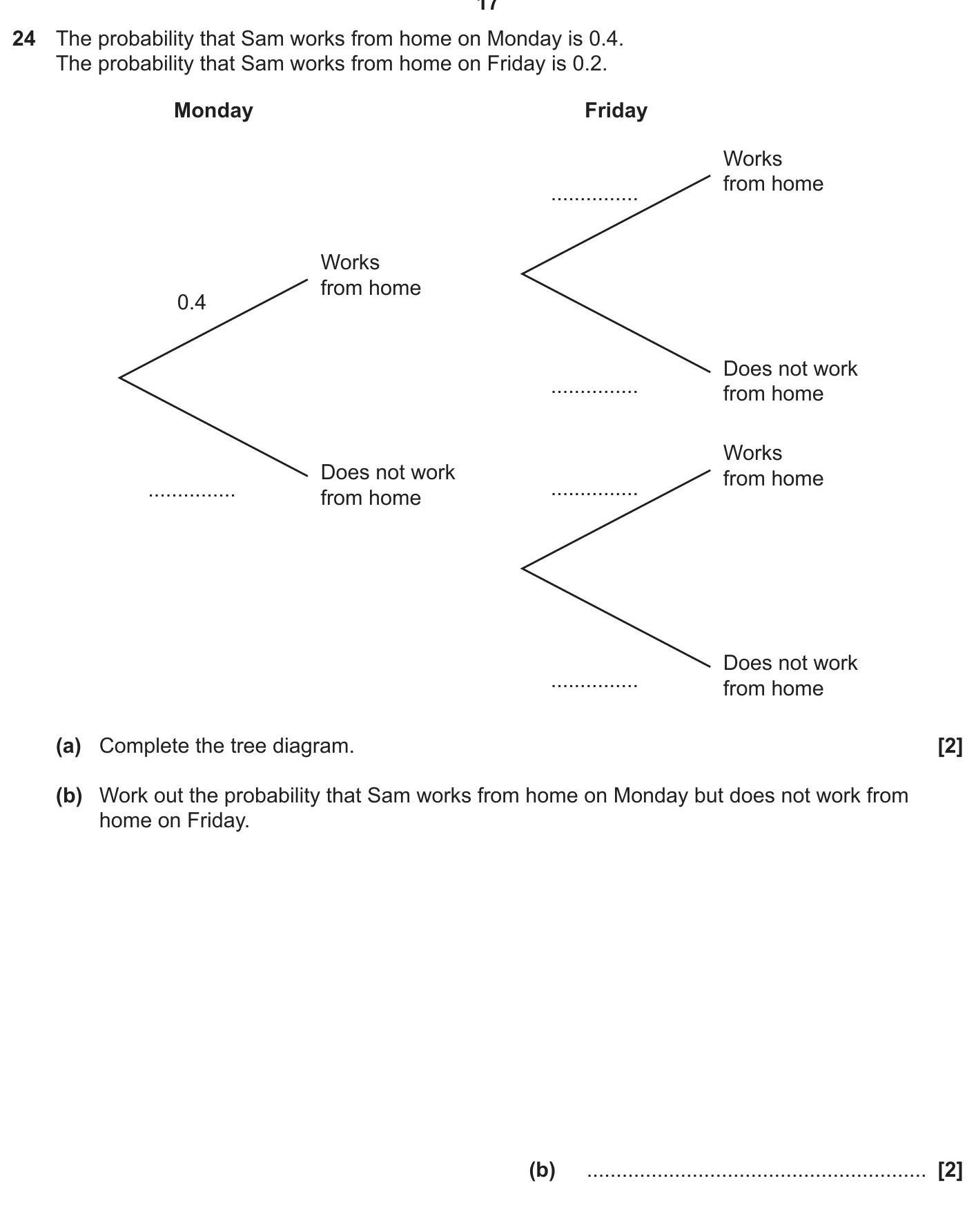
The probability that Sam works from home on Monday is 0.4. The probability that Sam works from home on Friday is 0.2. (a) Complete the tree diagram. (b) Work out t... show full transcript
Worked Solution & Example Answer:The probability that Sam works from home on Monday is 0.4 - OCR - GCSE Maths - Question 24 - 2023 - Paper 1
Step 1
Complete the tree diagram.
Answer
To complete the tree diagram, we need to determine the probabilities of Sam not working from home on both days.
-
The probability that Sam does not work from home on Monday is given by:
-
The probability that Sam works from home on Friday is 0.2, so the probability that he does not work from home on Friday is:
Therefore, the completed tree diagram will look like this:
Monday Friday
------- -------
Works from home 0.4 --> Works from home 0.2
| |
| |
| Does not work from home 0.8
| |
Does not work from home 0.6 -->
Step 2
Work out the probability that Sam works from home on Monday but does not work from home on Friday.
Answer
To find the probability that Sam works from home on Monday but does not work from home on Friday, we multiply the probabilities from the tree diagram:
- The probability that Sam works from home on Monday is 0.4.
- The probability that he does not work from home on Friday is 0.8.
Thus, the combined probability is:
Substituting the values we have:
Therefore, the probability that Sam works from home on Monday but does not work from home on Friday is 0.32.
